geometria astral: Do okregu o srodku S=(1,1) należy punkt A = (2,2). Oblicz pole P trojkąta równobocznego wpisanego w ten okrąg.

grabarz: a masz wynik?

astral: odpowiedz z książki cytuje:

	3
odp: P=		√3
	2

wskaówka : z warunków zadania promień okregu jest równy 1, a z zależności w trojkącie

	a√3		3		a2√3
równobocznym R=		mamy a =		oraz P =
	3		√3		4

Jak dla mnie to promień jest równy √2 a nie jeden i przecież nie możemy podstawić wzoru na wysokość trójkąta równobocznego za promień bo to się sobie nie równa. Dlatego daje bo rozwiązanie z ksiązki wydaje się złe i w ogóle całe zadanie nierealne.

grabarz: no ja to obliczylem ale mi troche inaczej to wyszlo, bo promien tez mi sie wydaje ze jest rowny √2, a wysokosc mozesz obliczyc wiedzac ze √2 stanowi ²₃ wysokosci. Nie wiem czy na pewno dobrze mowie ale ja bym to tak obliczyl

astral: no tez tak myślałem, ta odpowiedź mnie zmyliła ale widocznie błąd po ich stronie. To jest jakby co z zielonego zbioru podkowy. Dzięki i pozdro ; )

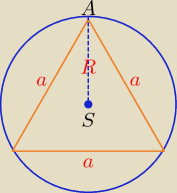
Bogdan: R = √1² + 1² = √2

	1		1
R =		a√3 ⇒ √2 =		a√3 / *√3 ⇒ a = √6
	3		3

	1		1
PΔ =		a2√3 =		*6*√3 = ...
	4		4