dziedzina sam:

	−3
y =		− √−x+4 prosze o sprawdzenie czy dobrze dziedzine wyliczyłem
	√x2−4

z pierwszego wyrazenia: (x−2)(x+2)≠0 x≠2 i x≠−2 oraz (x−2)(x+2)≥0 x≥2 i x≥−2 więc D=(−∞, −2) u (2, +∞) z drugiego wyrazenia: −x+4≥0 −x≥−4 x≤4 więc D=(−∞, 4> Tak więc wziąć to w całość to D=(−∞, −2) u (2, 4>

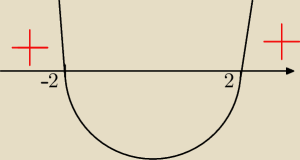
Godzio: (x − 2)(x + 2) ≥ 0 ⇒ x ∊ (−∞,−2> ∪ <2,∞) chodzi o zapis x ≥ 2 lub x ≤ −2 Reszta ok

sam: aha to fajno, no wlasnie ja tez nad tym myslalem, ale jak mam to rozumiec, bo popatrz jak ja tak to zabisze (x−2)(x+2)≥0 to przeciez nie mnoze ani nie dziele "x" przez minus i z czego to wynika ze znak sie zmienia... nie moglem tego rozkinic i dalej nie moge hhe

Godzio: x² − 4 ≥ 0 x² ≥ 4 /√ |x| ≥ 4 ⇔ x ≥ 2 lub x ≤ −2

sam: aha dzięki