Prostą k przesunięto o wektor Aska: proszę o pomoc, zadanie z geometrii analitycznej Prostą k przesunięto o wektor w=[4,3], a następnie otrzymany obraz przekształcono przez symetrię względem osi OX, uzyskując prostą l o równaniu 2x−3y+6=0.Wyznacz równanie prostej k.

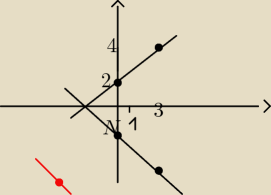
Raina: Najpierw zaznaczasz na osi znaną tobie prostą 2x−3y+6=0. Następnie jak widać na rysunku rysujesz obraz tej osi względem osi OX. Tzn., że przesuwasz dwa punkty które należą do prostej symetrycznie względem osi x, dlatego z punktu (0,2) robi się punkt (0,−2) a z punktu (3,4) robi się (3,−4). Prowadzisz prostą przez dwa nowe punkty. Dalej przesuwasz ten wykres o wektor teraz odwrotny niż ten, który został podany w zadaniu, czyli o wektor [−4,−3]. Dlatego znowu z punktów tym razem (0,−2) i (3,−4) robią się kolejno punkty (−4,−5) oraz (−1,−7). Aby wyznaczysz równanie prostej k wystarczy te dwa nowe nowe punkty włożyć w układ równań: −5=−4a+b −7=−a+b Odejmujemy stronami i mamy: 2=−3a −2/3=a i −7=−(−2/3) +b −7 −2/3=b −23/3=b a więc równanie prostej k wynosi y=−2/3x−23/3

Aska: bardzo dziękuję za obszerne wytłumaczenie