pole powierzchni wielościanu
prosze pomóżcie-poprawiam ocen: Oblicz pole powierzchni całkowitej ostrosłupa ściętego, którego krawędzie boczne mają tę samą
długość, wysokość ostrosłupa ma długość równą 4, a podstawy są trójkątami równobocznymi o
bokach długości odpowiednio 4 i 2.
15 gru 23:11
JeyAr: obliczasz pola obu trójkątów....o boku 2 i o boku 4
Ściany boczne są trapezami równoramiennymi....o wymiarach 4 na dole 2 na górze i x po bokach
Jak poznasz x to masz wymiary trapezów.....oblicz wtedy ich pola i koniec zadania
15 gru 23:39
Niunia85:
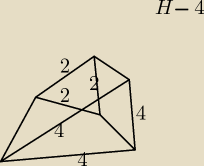
Pc=2Pp+4Pb
Pc=
√3+4
√3+4*12=48+5
√3
15 gru 23:40
JeyAr: pomyłka Niunia...
wysokość 4 to wysokość ostrosłupa a nie trapezu
15 gru 23:43
Niunia85: a no tak
15 gru 23:50
Niunia85: czyli trzeba wyliczyć ze wzoru na objętość ściętego?
15 gru 23:51
JeyAr: albo tak jak pisałem wyżej...ale nie chce mi się już rysować rysunku dlaczego takie
równanie....
15 gru 23:52
15 gru 23:53
wysokość trapezu: tzn w mianowaniku 2. chodzi mi o pierwszy komentarz
15 gru 23:54
Niunia85: u mnie czegoś takiego nie ma
15 gru 23:54
JeyAr:
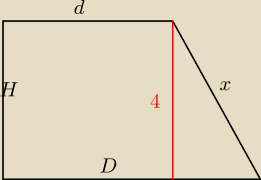
H=4 D−to 2/3 wysokości trójkąta w podstawie dolnej
d− 2/3 wysokości trójkąta w górnej podstawie
x− krawędź boczna albo boki trapezu
15 gru 23:55
wysokość trapezu: to h mi wyszlo √19 a to na pewno jest zle, bo wunik jest ze pole calkowite równe jesst 26√3
15 gru 23:57
wysokość trapezu: tzn x wyszlo mi 2√5 i później z tw pitagorasa obliczam h
h2 + 12 = (2√5)2 ... h = √19
15 gru 23:58
15 gru 23:58
JeyAr: potem Pitagorasem obliczasz X
15 gru 23:59
JeyAr:
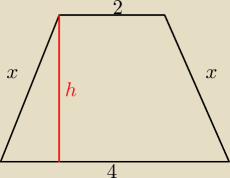
16 gru 00:01
JeyAr: a potem już tylko h i pole trapezu
16 gru 00:01
wysokość trapezu: nie wiem, nie pojmę tego ale mimo wszystko dziękuje
miłej nocy życze!
16 gru 00:02
16 gru 00:04
JeyAr: pole trapezu 1/2*(4+2)*h=√3
16 gru 00:05
JeyAr: jutro dokończę...idę lulu...
16 gru 00:07
Bogdan:
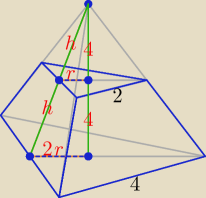
r − długość promienia okręgu wpisanego w trójkąt równoboczny o boku długości 2.
2r − długość promienia okręgu wpisanego w trójkąt równoboczny o boku długości 4.
| | 2 | | 2 | | 12 | |
2r = |
| *2*√3 = |
| √3, (2r)2 = |
| |
| | 6 | | 3 | | 9 | |
Z twierdzenia Pitagorasa w zielonym trójkącie:
| | 14√3 | | 7√3 | |
2h = √64 + 12/9 = |
| ⇒ h = |
| |
| | 3 | | 3 | |
| | 1 | | 7√3 | |
Pole powierzchni trapezu PT = |
| *6* |
| = 7√3 |
| | 2 | | 3 | |
| | 1 | | 1 | |
Pole powierzchni podstaw PP = |
| *16√3 + |
| *4√3 = 5√3 |
| | 4 | | 4 | |
Pole powierzchni całkowitej P = 3*7
√3 + 5
√3 = 26
√3
16 gru 00:24