zadania po części konkursowe!.. proszę o pomoc,
tomq: 1.Do liczby dwucyfrowej dopisano na koncu 5. Otrzymana liczba trzycyfrowa jest o 293 wieksza od
poczatkowej liczby. Znajdz obie liczby.
Myślałem nad zapisem
xy5= 100x+10y+5
xy5=293+xy
100x+10y+5=293+xy
i jak teraz mam z tego policzyć x i y? ^^
2. Karol wylozyl prostokatny plac o wymiarach 5m na 10m kostka brukowa w dwoch kolorach: na
zewnatrz obwodka o jednakowej szerokosci w kolorze czerwonym, wewnatrz prostokat w kolorze
bezowym. Oblicz szerokosc obwodki, jesli Karol wylozyl 26 m kwadr. kostki w kolorze czerwonym.
3. Oblicz pole rombu, ktorego jedna przekatna jest o 1cm dłuzsza, a druga o 3 cm dluzsza od
dlugosci boku rombu.
15 gru 14:06
tomq: przygotowujące oczywiście

proszę o pomoc.
15 gru 14:23
Eta:
zad.1/
10x+ y −−− szukana liczba
100x+10y+5 = 10x+y+ 293
90x+ 9y= 288 / :9
10x+y= 32 −−− szukana liczba
odp: taką liczbą jest liczba 32
15 gru 14:24
tomq: dzięki Eta

już akurat do tego doszedłem. A co z resztą? Masz jakiś pomysł?
15 gru 14:30
Eta:
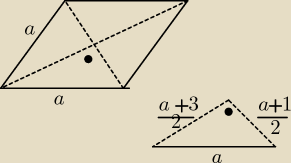
zad,3/
a −−− dł. bou rombu, a>0
e= a+1 , f= a+3
z tw. Pitagorasa:
| | a+1 | | a+3 | |
( |
| )2+ ( |
| )2= a2
|
| | 2 | | 2 | |
to:
(a+1)
2+(a+3)
2= 4a
2
dokończ, pamiętając,że a>0
15 gru 14:39
ric: a
2+2a+1+a
2+6a+9=4a
2
2a
2+8a+10=4a
2
−2a
2+8a+10=0
Δ=64−4*10*(−2)=144
√Δ=12
a1=5
a2=−1 odrzucamy
więc a =5?

dłuższa przekątna 8, a krótsza 6?
15 gru 14:44
tomq: a na 2 ma ktoś pomysł?

15 gru 14:51
Eta:
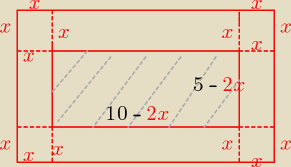
P placu = 5*10= 50 m
2
P( beżowego) = 50−26= 24m
2
wymiary beżowego: 10−2x, 5−2x , dla x € ( 2,5 ; 5)
P(beżowego) = ( 10−2x)(5−2x)= 24
rozwiąż to równane, pamiętaj,że
x€ ( 2,5 ; 5)

15 gru 15:09
tomq: 4x
2−30x+36=0
Δ=576
√Δ=24
co ja robie źle? : D
15 gru 15:35
tomq: pomylka

juz wiem
15 gru 15:42
Eta:
2x2 −15x +13=0
15 gru 15:44
tomq: ale znów:
Δ=121
√Δ=11
x1=15−11/4=4/4=1
x2=15+11/4=26/4=6,5
15 gru 16:00
Eta:
Echh sorry

pomyliłam się w założeniu
10−2x >0 i 5− 2x >0 i x >0
x <5 i x <2,5 i x >0
to oczywiście , że
x€ ( 0; 2,5)
teraz pasuje tylko x = 1
15 gru 16:19
 proszę o pomoc.
proszę o pomoc.
 już akurat do tego doszedłem. A co z resztą? Masz jakiś pomysł?
już akurat do tego doszedłem. A co z resztą? Masz jakiś pomysł?
 zad,3/
zad,3/
 dłuższa przekątna 8, a krótsza 6?
dłuższa przekątna 8, a krótsza 6?

 P placu = 5*10= 50 m2
P( beżowego) = 50−26= 24m2
wymiary beżowego: 10−2x, 5−2x , dla x € ( 2,5 ; 5)
P(beżowego) = ( 10−2x)(5−2x)= 24
rozwiąż to równane, pamiętaj,że x€ ( 2,5 ; 5)
P placu = 5*10= 50 m2
P( beżowego) = 50−26= 24m2
wymiary beżowego: 10−2x, 5−2x , dla x € ( 2,5 ; 5)
P(beżowego) = ( 10−2x)(5−2x)= 24
rozwiąż to równane, pamiętaj,że x€ ( 2,5 ; 5)

 juz wiem
juz wiem
 pomyliłam się w założeniu
10−2x >0 i 5− 2x >0 i x >0
x <5 i x <2,5 i x >0
to oczywiście , że x€ ( 0; 2,5)
teraz pasuje tylko x = 1
pomyliłam się w założeniu
10−2x >0 i 5− 2x >0 i x >0
x <5 i x <2,5 i x >0
to oczywiście , że x€ ( 0; 2,5)
teraz pasuje tylko x = 1