stereometria - kto podoła? piter: Ostrosłup z trójkątem w podstawie o bokach 6, 6 i 8. Wszystkie krawędzie boczne po 9. Oblicz objętość. HOW? Będę wdzięczny za pomoc, bo zadanie 2 dzień nie daje mi spokoju, nie wiem co przeoczyłem. Pozdrawiam!

michal:

	1
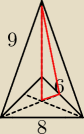
Musisz wziąć pod uwagę ten oto czerwony trójkąt. Obliczyć wysokość ściany bocznej,
	3

przekątnej trójkąta w podstawie i z tw. Pitagorasa znaleźć wysokość.

a: Podpowiedź: na podstawie ostrosłupa można opisać okrąg

piter: Dzięki za szybką odpowiedź, Chciałem wyjść od tej wysokości, ale zauważyłem że w podstawie mam trójkąt równoramienny a nie równoboczny, w którym wysokości nie dzielą się w takim ładnym stosunku. Niemniej mam inną koncepcję opartą na znalezieniu wysokości w ścianie bocznej o podstawie długości 8, oraz wysokości w podstawie trójkąta opuszczonej na bok długości 8. Da mi to przekrój przez ostrosłup, który wysokość tego ostrosłupa dzieli na 2 trójkąty prostokątne, ale nie wiem w jakim stosunku. Układ równań z pitagorasów i mam niezbędną do obliczenia objętości wysokość ostrosłupa. Policzę i dam znać czy wyszło (jakby kogoś to w ogóle obchodziło... ) piter

piter: Tak jak pisałem wyżej: Wysokość ściany bocznej o podstawie 8 − √65 Wysokość trójkąta w podstawie opuszczona na bok o długości 8 − 2√5 Dostajemy przekrój przez ostrosłup (będący trójkątem) o bokach 9 (krawędź boczna z wierzchołka podstawy w którym schodzą się oba boki o długości 6), √65 i podstawie 2√5. Rzut na podstawę wierzchołka tego trójkąta daje nam 2 trójkąty prostokątne i dzieli ją w nieznanym stosunku. Stąd piszemy twierdzenie Pitagorasa dla tych trójkątów, uwzględniając fakt niewiadomego podziału podstawy i wyliczamy H (wys. ostrosłupa) i x − zmienną użytą do uwzględnienia faktu przytoczonego wcześniej (na zielono w poniższym układzie równań). (wiem że czytelniej było by zobrazować to wszystko rysunkiem ale pomimo iż moduł graficzny nie jest skomplikowany w obsłudze to nie mogę umieścić na nim oznaczeń tak jak bym chciał, a że jestem rysunkowym pedantem to musi wystarczyć opis) Układ równań:

⎧	92=(2√5−x)2+H2
⎩	(√65)2=x2+H2

Po użyciu wzoru skróconego mnożenia i przekształceniach otrzymujemy:

	√5		18√5
x=		H=
	5		5

Znając wysokość ostrosłupa możemy obliczyć objętość:

	1		1		18√5
V=		*		*2√5*8*		= 48
	3		2		5

pozdrawiam piter