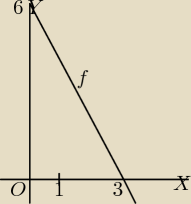
funkcja ania: na rysunku przedstawiono wykres funkcji liniowej f a) wyznacz wzór funkcji f b) sprawdz czy dla argumentu x=1/√2−1 wartośc funkcji f jest równa 4−2√2

Tadeo: Napisz równanie prostej przechodzącej prze te dwa punkty. Potem sprawdź czy spełniają je x i y z Twego puntu b)

monia:

niuś niuś: Wiem że "odgrzewam kotleta" ale jak by ktoś jeszcze potrzebował rozwiązania to: Mamy dwa punkty A[3;0] oraz B[0;6] Po podstawieniu ich do wzoru na prostą y=ax+b tworzymy układ równań: 0 = 3a + b b = 6 zatem podstawiamy nasze b do pierwszego równania i otrzymujemy: 0 = 3a+6 ⇔ −3a = 6 / −3 ⇔ a= −2 A zatem punkty naszej prostej to a = −2 i b= 6 ⇔ y=−2x+6 Odp: Wzór funkcji to y=−2x+6 Podstawiamy teraz naszego x pod równanie funkcji: f(x)=−2*1/√2−1 mnożymy to teraz przez √2−1/√2+1 i po skróceniu otrzymujemy f(x)=−2√2−2+6 a zatem f(x)=4−2√2 Odp: tak równa się.

anka: dlaczego po skróceniu otrzymujemy f(x)=−2√2−2+6 ?