dziedzina sam: Mam takie pytanko: dziedziną funkcji liniowej jest zawsze zbiór liczb rzeczywistych? Nie musimy nic wyliczać (tak jak w przypadku funkcji kwadratowej), by obliczyć dziedzinę?

martuś: zalezy jak wyglda ta funkcja

fajny: Dla kwadratowej też zwykle dziedziną są rzeczywiste, ale tak jak twierdzi martuś, wszystko zależy jak ta funkcja wygląda

sam: a gdy mam funkcje takiej postaci f(x)=−2x³ +5x−3 i miejsca zerowe to: x₁=1¹₂ oraz x₂=1 to dziedziną jest D=R\{1; 1¹₂} ?

fajny: nie D=R miejsca zerowe nie mają nic wspólnego z dziedziną

sam: aha, a jak mam wyliczyć dziedzinę z y= 2e^x2 ?

martuś: ej fajny pomozesz mi

fajny: sam, tego nie umiem − nie miałem jeszcze wykładniczych

martuś: nie chodzi mi o kat nachylenia a dokladnie przekatna jest nachylona do plaszczyzny podstawy walca

fajny: jak dokładnie brzmi treść?

martuś: przekrój osiowy walca jest prostokatem o przeatnej dl 6√3. przekatna jest nachylona do plaszczyzny podstawy walca pod katem π\6 rad. obl. obj . i p.pow.cał.walca

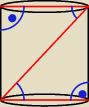
fajny: rysunek

fajny: biebieskie kąty (te, które nie są proste) to właśnie to π/6 rad

martuś: ok i patrz mam przekatna co nie i moge z trygometri ale nie znam a ani b?

martuś: a to akurat wiem

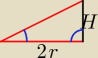
fajny: π/6 rad = 30 st. Z własności trójkąta 30,60,90: H = 3√3 2r = 9

martuś: a mozesz to rozpisac

martuś: albo wiesz nie moge dojsc ktos mi wytlumaczyl i nie wiem Zad. przekrój osiowy walca jest prostokatem o przeatnej dl 6√3. przekatna jest nachylona do plaszczyzny podstawy walca pod katem π\6 rad. obl. obj . i p.pow.cał.walca

fajny: 6√6 = 2H H = 3√3 H√3 = 2r 2r = 3√3*√3 = 9

martuś: 6√3 przeciez

martuś: kloki juz wiem ale ja jestem glupia ja skozystalam z cos30st

martuś: mam pytanie pole na to cudo jest P= 2*pi*r*h czyli 2*oi*3*3√3

fajny: pole pow. całkowit. P = P pow. bocz. + 2 * P podst. P pow. bocz. = 2πr*h P podst. = πr²

martuś: czy;i to r to nie R bo kurde czyli to 9 jest jest to r ktore podkladam na wzoru bo ja myslalm o R

fajny: r=R 2πr*h to wzór na pole pow. bocznej walca, a ty musisz policzyć ppole pow. całkowitej, więc musisz jeszcze dodać do tego pola podstaw

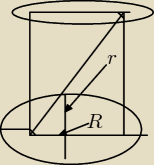
martuś: chodzilo ci o to ktore

martuś: npo to juz wiem wlasnie ze nie bo male r to jest promien a duze R to srednica czyli do wzoru daje 9 ale przez jest r czyli promien

fajny: jeżeli przyjmiesz, że: promień r = 4,5 średnica R = 2r = 9 to wzór masz 2πr*h albo πRh. Jak wolisz.

martuś: nie bo sa inne wyniki jak przyjme ze 9 to to jest 2pi * 9*3√3= 54√3pi a w tym drugim to 2pi*4,5*3√3= 27√3pi

fajny: jak liczysz ze średnicą, to bez tej '2' na początku πRh = π*9*3√3 = 27π√3

martuś: no o to chodzilo an pocztku mi

martuś: √108 ile to

fajny: 108 = 9 * 11 √108 = 3√11

martuś: oki dzieki

martuś: ty chodzisz do szkoly jakiej

fajny: fajnej

martuś: hehe no to maturanej

fajny: zgadłaś!

martuś: ooale fajnie

martuś: Lo czy tech

fajny: a co?

martuś: nic tak pytam

fajny: lo, ale nie wiem, jakie to ma znaczenie...

martuś: to po co piszesz

fajny: bo pytasz

martuś: no ale nie musisz pisac

Paulina: to może się dołożę? nie wiem jak to zadanie w ogóle zacząć... Punkt O jest środkiem szescianu (punktem przecięcia przekątnych sześcianu i Srodkiem koła wpisanego w ten sześcian) o krawędzi a. Oblicz promień sfery o środku w punkcie O, która jest styczna do wszystkich ścian tego sześcianu.

fajny: zacznij najlepiej od rysunku

Paulina: już mam ale zero danych. Wiem, że promień to połowa a

fajny: Skoro dane masz tylko "literkowe" to wynik też musi być "literkowy". Musisz zadbać tylko o to, żeby w wyniku końcowym nie pojawiły się inne literki niż te z treści zadania. U ciebie wszystko się zgadza. Odp.: Promień tej sfery wynosi a/2.

Paulina: takie to proste? tyle, że w poleceniu jest oblicz nie wyznacz>

fajny: No ale spójrz na to logicznie: nie możesz nic obliczyć, skoro nie masz żadnych danych liczbowych.

Paulina: właściwie nie Dzięki