lfunkcje
klaudia: zbiorem wartości funkcji f(x)=2x+1
jest a.(1;+nies)
b.zbiór liczb rzeczywistych
c. {1;+nies}
d. zbiór pusty
14 gru 11:51
sushi_ gg6397228:
ciekawy jest ten zbior w "c" dwuelementowy {1 , ∞}
14 gru 11:58
klaudia: jak to obliczyć
14 gru 11:59
sushi_ gg6397228:
y=2
x −−−> wiesz jak wyglada wykres tej funkcji
14 gru 12:00
klaudia: nie
14 gru 12:01
sushi_ gg6397228:
a wykres y=ax gdy a> 1
14 gru 12:02
klaudia: też nie
14 gru 12:02
14 gru 12:02
sushi_ gg6397228:
widzimy juz jak wyglada wykres funkcji
14 gru 12:04
klaudia: nic z tego nie rozumiem
14 gru 12:04
sushi_ gg6397228: masz podany wzor
y=a
x i wykres , wiec czego nie rozumiesz
?
14 gru 12:06
klaudia: namalowałam wykres wyszła mi funkcja rosnąca, niewiem dlaczego od1 , wiem że do +
nieskonczoności
14 gru 12:16
sushi_ gg6397228:
najpierw zadalem pytanie do tego wykresu ze strony
a Ty sie juz pospieszylas
mamy wykres y=2
x nastepnie przesuwamy go o 1 do gory i mamy wykres f(x)=2
x+1
14 gru 12:22
sushi_ gg6397228:
y=2
x
jezeli x−−> −
∞, do czego dązy "y"
patrz rysunek z linku
14 gru 12:23
klaudia: przecina oś y w punkcie 1
14 gru 12:26
sushi_ gg6397228: nie odpowiadasz na pytania
!, wiec jak mozna Tobie pomóc
14 gru 12:28
klaudia: do + nieskonczoności, do góry
14 gru 12:31
sushi_ gg6397228:
co ja napisalem o 12.23
14 gru 12:32
sushi_ gg6397228:
tak sobie dla JAJ postawilem " −" przed "∞"
14 gru 12:33
klaudia: niewiem
14 gru 12:34
klaudia: od − nieskonczoności do +nieskonczoności
14 gru 12:35
14 gru 12:39
sushi_ gg6397228:
jezeli x−−> − ∞, to do czego dązy "y"
(patrzymy sie na wykres funkcji dla "x" ktore ida sobie w lewa strone, do czego idzie sobie
wykres funkcji)
14 gru 12:41
klaudia: do −∞
14 gru 12:43
sushi_ gg6397228:
to Ty chyba patrzysz na inny rysunek
14 gru 12:44
sushi_ gg6397228:
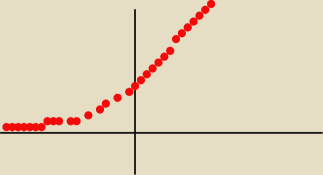
powiedz mi gdzie tu widzisz
y −−> − ∞
14 gru 12:45
klaudia: powiedz do czego dązy
14 gru 12:45
klaudia: muszę leciec do szkoły , może później skonczymy
narazie dzięki
14 gru 12:48