sae proszę pomóżcie :))): oblicz pole powierzchni bocznej graniastosłupa trójkątengo prawidłowego wiedząc, że promień okręgu opisanego na jego podstawie ma długość równą 6., a przekątna ściany bocznej ma długość 12.

rzadko proszę pomoc: Bogdan, gdzie jesteś?Chyba nikt, poza Tobą tego nie zrobi

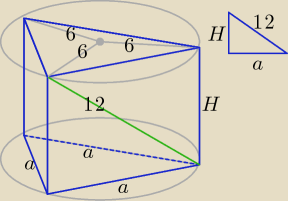
Bogdan: To łatwe zadanie na poziomie III klasy gimnazjum. Wystarczy zastosować twierdzenie Pitagorasa oraz zależności:

	1
− długość promienia okręgu opisanego na trójkącie prostokątnym R =		a√3,
	3

stąd trzeba wyznaczyć a dla R = 6. − mając a obliczamy długość H: H = √12² − a² − pole powierzchni bocznej P_B = 3aH Więcej wiary w siebie życzę

Eta: Bogdanie..... pozwól,że poprawię literówkę

	1
− "długość promienia okręgu opisanego na trójkącierównobocznym R=		a√3 "
	3

Bogdan: Dobry wieczór Eto . Dziękuje za poprawienie mojego chochlika.