Stereometria Anusiak: suma długości wszystkich krawędzi graniastosłupa prawidłowego trójkątnego jest równa 42 cm. a pole powierzchni bocznej wynosi 72cm2.Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy oraz środek przeciwległej krawędzi bocznej i jako przekrój otrzymano trójkąt równoramienny . Oblicz cosinusy kątów tego trójkąta.(rozpatrz dwie możliwości)

Anusiak: pomoże ktoś

Anusiak:

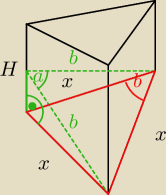
a: Z treści zadania: 6x + 3H = 42 H + 2x = 14 H = 14 − 2x −−−−−−− 3xH = 72 xH = 24 x(14−2x) = 24 x² + −7x + 12 = 0 √Δ = 1

	7 + 1
x1 =		= 4
	2

	7−1
x2 =		= 3
	2

H₁ = 14 − 8 = 6 H₂ = 14 − 6 = 8 −−−−− Z trójkąta prostokątnego: 1. 3² + 4² = b² ⇒ b = 5 2. 4² + 3² = b² ⇒ b = 5 Wartości cosinusów obliczysz z tw. cosinusów: 1. Pierwszy przypadek: dla x = 4, H = 6 4² = 5² + 5² − 50cosα − 34 = − 50cosα

	34		17
cosα =		=
	50		25

5² = 4² + 5² − 40cosβ −16 = −40cosβ

	16		2
cosβ =		=
	40		5

Drugi przypadek zostawiam do obliczenia Tobie

Maria: Suma długości wszystko krawędzi graniastos prawie trójkątnego wynosi 3 jaką największą objętość może mieć ten graniastos

arengamerpl: bardzo fajne zadanko, dzięki tobie nauczyłem się matematyki 😎👍