Równanie okręgu w ujęciu analitycznym :) ewa: Wyznacz środek i promień okręgu o równaniu x² + y² −4x−2y −4=0 oraz równania stycznych , równoległych do osi OY

sushi_ gg6397228: wzor na okreg znasz

ewa: x² + y² = r²

sushi_ gg6397228: (x−a)² +(y−b)²=r² taki jest wzor ,a po rozpisaniu x² −2ax+a² +y² −2by +b²=r² −−> mamy taka postac w zadaniu −2ax=== −4x −2by===−2y porownujemy odpowiednie wielkosci−−> wyliczamy "a" i "b" x² −2ax+a² +y² −2by +b²=r² x² −2ax+a² +y² −2by +b²−r²=0 x² −2ax+y² −2by + a²+b²−r²=0 a²+b²−r² === −4 (majac dane "a" i "b" łatwo wyliczysz "r" )

Basia: to jest równanie okręgu, którego środkiem jest S(0,0) a tu jest potrzebne równanie okręgu o środku S(a,b)

ewa: wyszło mi S= (2,1) , a r=3 Dobrze? Ale nie wiem jak obliczyć te styczne

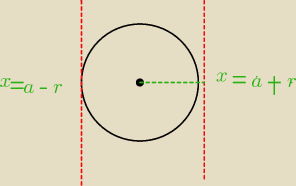
sushi_ gg6397228: tak to styczne beda postaci x= liczba

ewa: czyli x= −1 i x =5 czy tak?