;)
KM: Banalne pytanie
x∊B ∧ x∉C
czyli x∊(B\C) czy x∊(B∧C)?
13 gru 00:38
aga116: x∊(B\C)
13 gru 00:39
aga116: x∊(B\C)⇔x∊B ∧ x∉C⇔x∊B ∧ ¬x∊C tak to wyglada
13 gru 00:41
KM: A jak x∊B ∨ x∉C to wtedy x∊(B∧C)?
13 gru 00:41
aga116: nie
bo tu masz alternatywe wiec nagle nie moze Ci sie zrobic koniunkcja
13 gru 00:43
KM: No bo mam wykazać, że A∨(B\C)=[(A∨B)\C]∨(A∧C)
Rozpisuję lewą stronę na A∨(B\C)⇔(x∊A∨x∊B)∧(x∉B∨x∊C) i tam jest właśnie x∉B∨x∊C
13 gru 00:50
aga116:
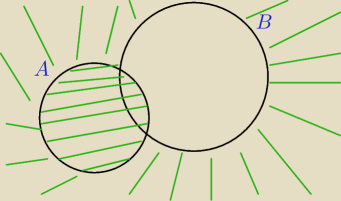
tak przedstawia sie graficznie x∊A v x∉B
13 gru 01:04
aga116: czyli obejmuje tu zbior A i dopelnienie B
13 gru 01:05
aga116: sprobuj sobie rozpisac prawa strone rownania
13 gru 01:06
KM: zaraz spróbuje pokombinować z prawa strona
13 gru 01:07
KM: [(A∨B)\C]∨(A∧C)
[(x∊A∨x∊B)∧x∉C]∨ (x∊A∧x∊C) ⇔[x∊A ∧ x∉C ∨ x∊B ∧ x∉C]∨ (x∊A∧x∊C) ⇔ [x∊(A\C) ∨ x∊(B\C)] ∨
(x∊A∧x∊C)
Nie wiem chyba źle to robię, bo za dużo tych nawiasów
13 gru 01:12
Basia:
dobrze jest ale co masz pokazać ?
to się dalej rozpisze tak:
x∊(A/C)∪(A∩C) ∨ x∊(B/C} ⇔
x∊A∪(B/C)
ale nie wiem czy o to chodziło
13 gru 07:01
KM: Ok, po prostu nie wiedziałam że (A\C)∪(A∩C) można zapisać jako A, ale w sumie to jest logiczne
Dzięki wszystkim za pomoc
13 gru 20:02