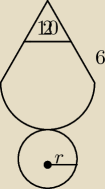
Stożek - bryły obrotowe Whizzer: Proszę o wytłumaczenie tego zadania krok po kroku, dlaczego to jest tak zrobione. Bo mam to rozwiązane tylko nie wiem co z czego, jak i po co. Zad. Na rysunku przedstawiono wycinek koła, który po zwinięciu jest powierzchnią boczną stożka. Oblicz pole podstawy i pole powierzchni całkowitej tego stożka. Pierwsze mam obl. długość łuku ł= ¹₃ * 2π*6=4π a potem promień r 4π=2πr r=2 Potem już te pola oblicze ale tego początku nie rozumiem, obliczenia łuku i promienia. A potem mam jeszcze takie jedno podobne zadanie. Powierzchnią boczną stożka po rozwinięciu jest wycinek koła o kącie 60 stopni i promieniu 12. Oblicz pole podstawy tego stożka. Rysunek jest taki sam jak wyżej i łuk jest liczony: ł= ³₄*2π*12= 18π 18π=2πr r=9 Tam 6 było jako tworząca a tu 12 jako promień i się podstawia tak samo.?

Whizzer: Pomoże ktoś?

Edi: Jeśli chodzi o pierwsze zadanie, to długość łuku liczymy z wzoru ł=α/360*2*π*r, a zatem wstawiasz za α 120( po skróceniu otrzymujesz 1/3), a za r wstawiasz 6 i wszystko wychodzi jak trzeba otrzymujesz zatem, że długość łuku wynosi 4π, a jest to jednocześnie tyle samo co obwód koła w podstawie stożka aby obliczyć promień podstawy wystarczy do wzoru na obwód koła O=2*π*r wstawić za obwód 4π i po wykonaniu działania otrzymujesz, że r=2.

Edi: Tworząca stożka jest promieniem wycinka koła, który otrzymuje się po rozwinięciu powierzchni bocznej stożka