dzielenie wielomianow Dzasta: wielomian W(x)=x3 −(a+b)x2−(a−b)x+3, xeR jest podzielny przez wielomian P(x)= x2−4x+3. wyznacz a i b, a następnie rozwiąż nierówność W(x)>0

grey: jak to zrobić? ; p

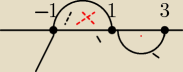
grey: P(x)=(x−1)(x−3) W(1)=0 W(3)=0 0=1−(a+b)−(a−b)+3 0=27−9(a+b)−3(a−b)+3 −4=−a−b−a+b 0=27−9a−9b−3a+3b+3 −4=−2a 0=30−12a−6b/:3 a=2 0=10−4a−2b a=2 −10=−4a−2b a=2 b=1 W(x)=x³−3x²−x+3=x²(x−3)−(x−3)=(x²−1)(x−3) (x²−1)(x−3)>0 (x−1)(x+1)(x−3)>0 x1=1 x2=−1 x3=3 x∊(−1,1) Mogłem się machnąć

Dzasta: Jesteś bogiem ^^ dzięki ; p