nierówności wielomianowe z wartością bezwzględna
messie: 3x2 ≤ |x3 − 4x|
bardzo proszę o pomoc w rozwiązaniu.
12 gru 16:52
Godzio:
1o x3 − 4x ≥ 0 ⇒ x ∊ ....
3x2 ≤ x3 − 4x
0 ≤ x3 − 3x2 − 4x = x(x2 − 3x − 4) ⇒ x ∊ .... sprawdź czy rozwiązanie zawiera się w
przedziale który badasz
2o x3 − 4x < 0 ⇒ x ∊ ...
3x2 ≤ −x3 + 4X
x3 + 3x2 + 4x ≤ 0
x(x2 + 3x + 4) ≤ 0 ⇒ x ∊ .... i tak samo jak wyżej
12 gru 16:55
konrad509: 3x2 ≤ |x3 − 4x|
x3−4x≥3x2
x3−3x2−4x≥0
x3+x2−4x2−4x≥0
x2(x+1)−4x(x+1)≥0
(x2−4x)(x+1)≥0
x(x−4)(x+1)≥0
x=0 x=4 x=−1
rys.1
x∊<−1,0>u<4,+∞>
x3−4x≤−3x2
x3+3x2−4x≤0
x3−x2+4x2−4x≤0
x2(x−1)+4x(x−1)≤0
(x2+4x)(x−1)≤0
x(x+4)(x−1)≤0
x=0 x=−4 x=1
x∊(−∞,−4>u<0,1>
x∊<−1,0>u<4,+∞)u(−∞,−4>u<0,1>
x∊(−∞,−4>u<−1,1>u<4,+∞) <−− ostateczne rozwiązanie
12 gru 17:14
konrad509:
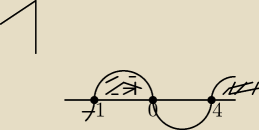
12 gru 17:19
konrad509: Chciałem narysować drugi rysunek, ale nie mam cierpliwości. Ten edytor to jest porażka...
12 gru 17:24
