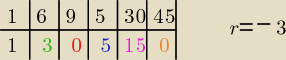wykaż że liczba r jest dwukrotnym pierwiastkiem wielmianu W(x), jeśli: alucha: w(x)=x⁵+6x⁴+9x³+5x²+30x+45, r=−3

Kejti: 1*(−3)+6=−3+6=3 3*(−3)+9=−9+9=0 0*(−3)+5=5 5*(−3)+30=−15+30=15 15*(−3)+45=−45+45=0 to ze schematu Hornera. Mam nadzieję, że widać jak dzieli się tym sposobem. Na końcu jest 0, co oznacza, że −3 jest pierwiastkiem tego wielomianu. Otrzymujemy z tego dzielenia wielomian o jeden stopień niższy: x⁴+3x³+5x+15 Należy to powtórzyć na otrzymanym wielomianie, gdzie również powinno wyjść na końcu zero.