Wyrazenia wymierne
Andrzej: Zbadaj monotoniczność funkcji
y =
to jest równanie nie wie działem jak inaczej napisać
12 gru 00:03
aga116: podstawowe pytanie: potrafisz obliczyc caleczke?
12 gru 00:07
Godzio:
aga tu chyba nie chodzi o całkę
tu raczej miało oznaczać jak klamra
12 gru 00:09
Andrzej: to zadanie ze szkoły średniej te symbole to po prostu układ równań
12 gru 00:09
aga116: aha
o lol
coz to ludzie nie wymysla
12 gru 00:14
Godzio:
x
1 > x
2 ⇒ x
1 − x
2 > 0
| | x1 − 1 | | x2 − 1 | |
f(x1) − f(x2) = |
| − |
| = |
| | x1 − 2 | | x2 − 2 | |
| | (x1 − 1)(x2 − 2) − (x2 − 1)(x1 − 2) | |
= |
| = |
| | (x1 − 2)(x2 − 2) | |
| | x1x2 − 2x1 − x2 + 2 − x1x2 + 2x2 + x1 − 2 | |
= |
| = |
| | (x1 − 2)(x2 − 2) | |
| | −2(x1 − x2) + x1 − x2 | |
= |
| = |
| | (x1 − 2)(x2 − 2) | |
| | −(x1 − x2) | |
= |
| |
| | (x1 − 2)(x2 − 2) | |
x
1 − x
2 > 0 ⇒ −(x
1 − x
2) < 0
x
1 − 2 < 0 , x
2 − 2 < 0 ⇒ (x
1 − 2)(x
2 − 2) > 0
| −(x1 − x2) | |
| < 0 |
| (x1 − 2)(x2 − 2) | |
Funkcja dla x < 2 jest malejąca, podobnie spróbuj zrobić dla x > 2
12 gru 00:14
Andrzej: prosze pomózcie z zadankiem mam 15 poodobnych przykładów
12 gru 00:14
Andrzej: o Kurde rzeźnik dzieki przeanalizuję
12 gru 00:15
aga116: Godzio moze zamiast mu rozwiazywac powinienes dac wskazowki niech sam na to wpadnie
inaczej
sie nie nauczy
12 gru 00:16
Andrzej: właśnie nic nie rozumie z tego
12 gru 00:17
aga116: Andrzej wiesz co to funkcja homograficzna?
12 gru 00:18
Godzio:
pokazałem jak zrobić pierwszą część teraz może spróbować drugą, ja chętnie wytłumaczę ale nie
teraz, dopiero jutro wieczorkiem nie mam już sił
12 gru 00:19
Andrzej: Wiem ale nigdy takich długich równań nie robiłem rysowałem hiperbole i tyle
12 gru 00:19
Godzio: Dobra zaraz powiem coś, tak na zakończenie dnia
12 gru 00:20
aga116: to narysuj sobie wykres tych funkcji dla odpowiednich przedzialow i z wykresu okresl
monotonicznosc
12 gru 00:21
Andrzej: będę wdzieczny
12 gru 00:21
Andrzej:
wykres mi wyszedł taki
Oczywiście nie przecina osi
12 gru 00:24
Godzio:
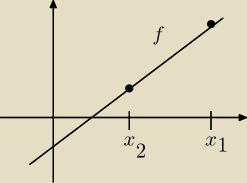
Weźmy sobie dowolną funkcję f, i 2 punkty f(x
1) i f(x
2) gdzie x
1 > x
2
Jeśli funkcja jest rosnąca to:
dla każdego x
1,x
2 ∊ D
f takich że x
1 > x
2 to f(x
1) − f(x
2) > 0
jeśli malejąca to
dla każdego x
1,x
2 ∊ D
f takich że x
1 > x
2 to f(x
1) − f(x
2) < 0
I dla przykładu weźmy funkcję liniową na całej dziedzinie, y = 5x + 2, należy sprawdzić jej
monotoniczność na podstawie definicji:
Wybieramy dowolne x
1,x
2 takie że x
1 > x
2 i sprawdzamy znak
f(x
1) − f(x
2) = 5x
1 + 2 − (5x
2 + 2) = 5x
1 + 2 − 5x
2 − 2 = 5x
1 − 5x
2 = 5(x
1 − x
2)
z założenia wiemy że x
1 > x
2 ⇒ x
1 − x
2 > 0 więc
f(x
1) − f(x
2) > 0 ⇒ funkcja jest rosnąca
12 gru 00:26
Godzio:
A ja w takim razie lecę spać
Dobranoc wszystkim
12 gru 00:27
Andrzej: dzeki 3m sie
12 gru 00:27
Andrzej: I jutro napisz mi jak możesz z jakich książek się uczyłeś maty
12 gru 00:28
aga116: lo Godzio boze ty sobie lubisz czlowieku zycie utrudniac
12 gru 00:30
aga116: Andrzej to mozna z wykresow odczytac
ucielo ci cos tam ale koncepcja jest dobra
12 gru 00:31
Andrzej: Kurcze ale jak by było w zadaniu odczytać z definicji to bym nie umiał
12 gru 00:32
aga116: no wiesz kwestia tego wszytskiego jest taka by robic jak najprosciej
skoro nie miales w
zadaniu zeby zrobic z definicji to nie rob
ale to tak na marginesie
w kazdym razie
dodatkowa wiedza Ci sie przyda i juz wiesz jak to z def. pojdzie
12 gru 00:34
Andrzej: Wiesz tej końcówki za bardzo nie rozumiem 5(x1 − x2) i skad mam wiedzieć ze jest rosnąca
?
12 gru 00:35
aga116: patrzysz na zalozenia, w tych zalozeniach masz ze x1>x2 oczywiscie oba x naleza do dziedziny
12 gru 00:36
aga116: i okreslasz znak calego wyrazenia
po prostu na na chlopski rozum podstawiasz sobie dowolne
liczby w miejsce x
1 i x
2 ktore naleza do dziedziny i okreslasz znak
12 gru 00:38
Andrzej: aga a ty co studiowałaś że tak mate ogarniasz
?
12 gru 00:42
aga116: ja nie studiowalam, ja studiuje matme stosowana
12 gru 00:45
Andrzej: o książki mi chodzi z jakich się uczyłaś tylko te co w szkole czy jakieś dodatkowe?
12 gru 00:49
adrian: Liczymy pochodne a nastepnie sprawdzamy kiedy f'(x) > 0 i f'(x) < 0. Gdy f'(x) > 0 w danym
przedziale to i f(x) > 0 dla tego przedziału, analogicznie gdy f'(x) < 0.Taki moj sposob.
12 gru 00:52
aga116: dobra adrian on w liceum jest
z ksiazek kiełbasy korzystalam
12 gru 00:55
Andrzej: ja mam kiełbase ale stoi 2 miechy na półce bo nic z niego nie rozumiałem narazie sie ucze z
tej strony
12 gru 00:56
aga116: a jestes na matmie podstawowej czy rozszerzonej?
12 gru 01:02
Andrzej: podstawowej + troche rozszerzenia chodzę do technikum ale chce pisać na maturze matme
rozszerzoną i własnie nie wiem z czego się uczyć
12 gru 01:04
aga116: ja sie z kielbasy uczylam i to mi wystarczylo... musisz zapytac maturzystow
12 gru 01:05
Andrzej: tylko że kiełbasa ma trudne zadania i wogóle nie ma wytłumaczenia. Podstawa u kiełbasy to u nas
rozszerzenie
12 gru 01:08
aga116: jak podstawa tam to u was rozszerzenie to szczerze CI powiem ciemno widze Twoja mature
roszszerzona jezeli sam sie nie przylozysz do nauki bo w szkole sie nie nauczysz
12 gru 01:10
Andrzej: dzień w dzień się ucze po kilka godzin zostało do matury 144 dni więc może dam radę
12 gru 01:13
aga116: coz powodzenie zyczyc
12 gru 01:15
Andrzej: danke ale na dobranoc mam dla ciebie ostatnie zadanie pomożesz bo kurde nie zasne
?
12 gru 01:15
aga116: jezei bede potrafic to pomoge
12 gru 01:17
Andrzej: Zbadaj monotonicznośc
∫ −x
2 + x dla x <= 2
y =
12 gru 01:17
aga116: tu podobnie jak w poprzednim, rysujesz wykres funkcji y=−x2+x dla x≤2 a dla x>2 rysujesz
wykres funkcji homograficznej, wiesz jak?
12 gru 01:19
Andrzej: no włąsnie tak robiłem i coś nie wychodziło mogła byś zrobić to zadanie ?
12 gru 01:20
aga116: ok
12 gru 01:22
12 gru 01:30
aga116: wiesz czemu tak?
ups w ostatnim poprawka ma byc (2,+∞)
12 gru 01:30
Andrzej: właśnie nie powiesz
?
12 gru 01:36
aga116: nie umiem tu rysowac
ok wiec tak: masz wykres paraboli wierzcholek jest w punkcie
(
12,
14)
miejsca zerowe to 0 i 1 w dwojce przyjmuje wartosc −2
sprobuj sobie na kartce to narysowac
ponadto ta druga funkcja to funkcja homograficzna i ona jest ograniczona przez dwie asymptoty
x=1 i y=−1, na przedziale x>2 jest rosnaca
12 gru 01:43
Andrzej: ok spróbuje l
12 gru 01:47
Andrzej: ok zrobiłem
12 gru 01:54
Andrzej: ok rozumiem dzieki
12 gru 01:56
aga116: spoko
12 gru 01:56
Andrzej: ostatnie pytanie jak pisze x > 2 to patrze na asymptoty czy na os?
12 gru 02:03
aga116: patrzysz na os OX
12 gru 10:42