Znajdź równanie prostej Milanos: Znajdź równanie prostej przechodzącej przez punkt A(5,2) i takiej, że odległości tej prostej od punktów B(−5,0) i C(13,−18) są sobie równe. Robię i nie wychodzi pomóżcie

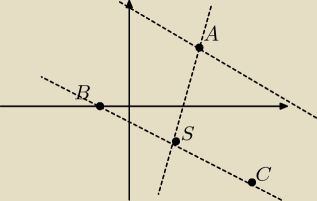
Grześ1992: ta prosta może między punktami Bi C albo równoleglęustawiona do punktów b i C. Musisz obliczyć równanie prostej B i C i obliczyć współrzędne środka prostej B i C (czyli punktu S) i obiczyć wtedy równanie prostej. Powinno Ci to coś pomóc, jakby co ja sam do końca nie wiem czy dobrze bym to zrobił, alę uważam, że to dobry tok rozumowania

Grześ1992: ta prosta może być między punktami B i C albo równolegle ustawiona do punktów B i C. Musisz obliczyć równanie prostej B i C i obliczyć współrzędne środka prostej B i C (czyli punktu S) i obiczyć wtedy równanie prostej. Powinno Ci to coś pomóc, jakby co ja sam do końca nie wiem czy dobrze bym to zrobił, alę uważam, że to dobry tok rozumowania

Grześ1992: ogólnie musisz obliczyć równania tych 3 prostych

Tragos: Niech m: y = ax + b − szukana prosta A(5,2) należy do m, więc 2 = 5a + b b = 2 − 5a y = ax − 5a + 2, sprowadzam do postaci ogólnej m: ax − y − 5a + 2 = 0 d(B, m) = d(C, m) zastosuj wzór tutaj wzór na odległość punktu od prostej

Grześ1992: masz może odpowiedzi ? mi wyszło y=−x+7

Tragos:

	|−5a − 5a + 2|
d(B, m) =
	√a2 + 1

	|13a + 18 − 5a + 2|
d(C, m) =
	√a2 + 1

|−5a − 5a + 2|		|13a + 18 − 5a + 2|
	=
√a2 + 1		√a2 + 1

|−5a − 5a + 2| = |13a + 18 − 5a + 2| |−10a + 2| = |8a + 20| |2(−5a + 1)| = |2(4a + 10)| |−5a + 1| = |4a + 10| / (..)², bo L > 0, P > 0 (−5a + 1)² = (4a+5)² 25a² − 10a + 1 = 16a² + 80a + 100 9a² − 90a − 99 = 0 / :9 a² − 10a − 11 = 0 Δ = 100 − 4*(−11) = 100 + 44 = 144 √Δ = 12

	10 − 12		−2
a1 =		=		= −1
	2		2

	10 + 12		22
a2 =		=		= 11
	2		2

a = −1 ⋁ a = 11 b = 2 − 5 * (−1) = 7 b = 2 − 5*11 = −53 y = −x + 7 y = 11x − 53

Grześ1992: no dokładnie tak tylko ja innym sposobem zrobiłem

Tragos: jeden błąd mi się wkradł, tam powinno być L ≥ 0, P ≥ 0

Grześ1992: trochę się namęczyłeś heh