...... Fela:D: wyznacz wysokosc prawidlowego ostroslupa trojkatnego ktorego krawedz podstawy ma dlugosc a a pole powierzchni bocznej jest dwa razy wieksze od pola podstawy. doszlam do tego ze h_{sciany bocznej}=a√3 i nie wiem co dalej?jak wyliczyc H duze?

a:

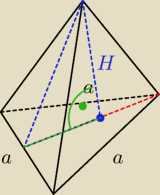
	a2√3
Pole podstawy =
	4

	a2√3
Pole powierzchni bocznej =
	2

	1
Odcinek zaznaczony na zielono stanowi		wysokości w trójkącie równobocznym (co prawda na
	3

rysunku tego nie widać, ale musisz mi uwierzyć na słowo )

	1		a√3		a√3
−		*		=
	3		2		6

	a√3
Obliczyłaś wysokość ściany bocznej −
	3

Z twierdzenia Pitagorasa obliczymy długość H:

	a√3		a√3
H2 + (		)2 = (		)2
	6		3

	a2		a2
H2 +		=
	12		3

	a2
H2 =
	4

	a
H =
	2

Fela:D: DZIEKUJE! JUZ WSZYTSKO ROZUMIEM!

Fela:D: nieee nie rozumiem dlaczego jest wysokosc ^a√3₃? mnie wyszlo samo a√3 i chyba dlatego cale zadania skopalam bo to ze jest 1/3 h to tez wbrew pozorom wiedzialam dlaczego jest ^a√3₃?

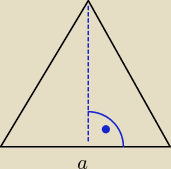a: Pole powierzchni bocznej jest równe sumie pól trójkątów, stanowiących ściany boczne. Są 3 takie trójkąty.

	1
Ich pole wyliczymy ze standardowego wzoru na pole trójąta −		* a * h, gdzie h − wysokość
	2

ściany bocznej

	1		a2√3
3 *		* a * h =
	2		2

3		a2√3
	a * h =
2		2

	a2√3		2
h =		*		a
	2		3

	a√3
h =
	3

Fela:D: O nieee..az wstyd przyznac co ja zrobilam tyle razy to liczylam i za kazdym razem bez tej 3 Przepraszam za zamieszanieDziękuję serdecznie jeszcze raz