Kasia: Zainteresowały mnie dwa zadania których kamil nie potrafi rozwiązać, chodzi dokładnie o te 2:
1. Dany jest ciąg określony wzorem an = −2n2 + 8n +10 . Które wyrazy tego ciągu są
nieujemne?
2. Ciąg ( an ) określony jest wzorem an = n4 − n3 − 27n + 27. Wyznacz wszystkie wyrazy tego
ciągu które są równe 0
byłabym wdzięcza gdyby ktoś pomógł teraz mi je rozwiązać, bo też nie mam pojęcia jak się za to
zabrać
9 gru 21:50
konrad509: 1. −2n2+8n+10≥0
2. n4−n3−27n+2=0
Trzeba rozwiązać te dwa równania. Te 'n' będące rozwiązaniami równań należące do N i większe od
zera będą numerami poszukiwanych wyrazów.
9 gru 21:54
M4ciek:
1.Nieujemne to znaczy ≥ 0.
−2n2 + 8n + 10 ≥ 0
Δ=144
√Δ=12
n1 = −1 ⇒ sprzeczne n2 = 5
Odp. 5 wyrazow tego ciagu jest nieujemnych.
9 gru 21:55
konrad509: Nie jest 5, tylko 1. 5 to numer wyrazu
9 gru 21:57
Godzio:
Tu akurat jest 5
ale ogólnie powinno się zapisać:
n ∊ <−1,5> i n ∊ N
+ ⇒ n ∊ {1,2,3,4,5}
9 gru 22:00
Eta:
1/ a
n ≥0 i n€N+
−2n
2 +8n +10 ≥0 / : (−2)
n
2 −4n −5 ≤0
Δ= 36
√Δ= 6
n
1= 5 n
2= −1
n€ ( −1, 5) i n€N+
to: n= {1,2,3,4}
takimi wyrazami spełniającymi warunki zad. są :
a
1, a
2, a
3, a
4
2/ a
n= 0 i n€N+
n
4 −n
3 −27n +27=0
n
3(n−1) −27( n−1)=0
( n−1)(n
3−27)=0
(n−1)( n−3)(n
2+3n+9)=0
n= 1 v n= 3 dla n
2 +3n +9=0 −−− brak rozwiazań w zb. N , bo Δ<0
odp: a
1 i a
3 −−− spełniają warunki zad.
9 gru 22:01
konrad509: Aha, ja nie obliczałem tylko na podstawie tego co M4aciek napisałem podałem.
9 gru 22:03
Godzio:
Eta małe zastrzeżenie ... w pierwszym przedziały domknięte
9 gru 22:06
9 gru 22:07
Eta:
1/ poprawka:
n€<−1, 5> i n€N+
to: n= {1,2,3,4,5}
odp: a
1, a
2, a
3, a
4, a
5
9 gru 22:09
Kasia: a skąd się wzieło −1, i 5?
9 gru 22:25
konrad509: Z −2n2 +8n +10. To są pierwiastki tego równania.
9 gru 22:29
max: 36
23 wrz 09:53
aaaa: A czy mógłby mi ktoś wyjaśnić jak rozwiązać takie zadanie :
Ciąg (an) jest określony wzorem an= 2n2 − 3n + 1 dla n ≥ 1. Zbiór wartości tego ciągu jest
podzbiorem zbioru
A. (o;∞)
B. <0;∞)
C. (−∞;0)
D. (−∞; 0>
5 kwi 18:01
Aga1.:
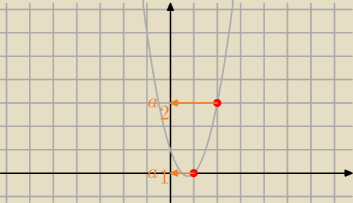
a
1=0, a
2=3, a
3= ... do którego przedziału należą te liczby?
5 kwi 18:19
aaaa: nie mam pojęcia, nadal tego nie ogarniam.
5 kwi 18:53
