Drobna sprawa :) Grześ: Pozdrawiam wszystkich forumowiczów. Mam do Was taką jedną sprawę. Staram się znaleźć jakichś ciekawych zagadnień związanych z funkcją kwadratową. Nie chodzi tu o żadne zwykłe równania, liczenie wartości itp. Chodzi mi o zastosowanie tych funkcji w praktyce. Wiem, że są tzw. zadania optymalizacyjne, ale mi chodzi o bardziej ciekawe treści. Ma ktoś z forumowiczów jakiś pomysł Czy jednak dla funkcji kwadratowej mało jest ciekawostek

Grześ: Podbijam, ma ktoś jakiś pomysł

Sylwia: Może być zadanie ze zbioru zadań do liceum z dwoma gwiazdkami?

Grześ: Jeśli chodzi o to, to ja akurat zbiór mam. Chodzi mi o jakieś ciekawe zagadnienia, ciekawostki itp. Wiem, że może być o to ciężko, ale może jednak da się coś znaleźć

Sylwia: A jakiego wydawnictwa? Bo tego zadania nie zrobiła nasza kobieta od matematyki.

Grześ: ja mam z pazdro, jak coś to z ciekawości rzuć mi zadankiem

Sylwia: Dobra, napisze, bo i tak nie mam co robic. 1.Ulica Klonowa jest prostopadła do ulicy Jesionowej, a centrum skrzyżowania ulic znajduje się w punkcie P. Samochód podróżujący na wschód ze stałą prędkością 40km/h mija punkt P w tym samym czasie, w którym samochód podróżujący na południe ze stałą prędkością 60km/h znajduje się dokładnie 5km na północ od punktu P. Oblicz po jakim czasie t[h] odległość między samochodami będzie najmniejsza i oszacuj tę odległość z dokładnością do jednego miejsca po przecinku. 2. O godzinie 13:00 statek B płynący na zachód ze stałą prędkością 20km/h znajduje się w odległości 10km od portu, zaś statek A płynący na północ ze stałą prędkością 40km/h znajduje się w odległości od portu 6 razy większej niż statek B. O której godzinie odległość między statkami będzie najmniejsza?

Sylwia: E... Ja tez Pazdro... Ale kaszana...

Grześ: akurat te widziałem w moim zbiorze. Napisałem że Pazdro Rozmyślam nad przedstawieniem może ich rozwiązań. A ktoś inny ma jakiś pomysł

Grześ: hihi, właśnie napisałem,

Sylwia: A rozwiązałeś je? Odpowiedzi są z tyłu, ale jak do nich dojść to nie wiem...

Sylwia: a dobry jestes z fizyki?

Grześ: Z tymi zadaniami problemu by nie był. Tylko nie wiem, ogólnie to po to założyłem temat, bo nauczycielka zaproponowała mi poprowadzić lekcje. No i właśnie szukam jakichs ciekawych materiałów

Grześ: Podbijam

Grześ: poodbijam, hmm

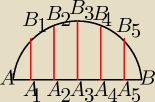
Mateusz: Most przedstawiony na rysunku przypomina kształtem część paraboli opisanej równaniem y =

	1		1
−		x2+		x pomost(jezdnia) ma długosc 108m i jest podtrzymywany przez pięć
	16		2

pionowych wieszaków: |A₁B₁| |A₂B₂| |A₃B₃| |A₄B₄| |A₅B₅| rozmiesczonych w równych odstępach oblicz ich długości 2) W ogrodzie zaprojektowano fontannę z której tryskające krople wody poruszają się po torach opisanych równaniami:

	2		3		1
y = −		x2+3x, y=−		x2+2x y=−		x2+x
	3		5		4

a) które równanie opisuje tor po którym krople spadają najdalej od środka fontanny? b) Które równanie opisuje tor po którym krople wody wznoszą się najwyzej Wiem że banalne ale zadnych ciekawszych nie znalazłempóki co

Mateusz: dorzuce jeszcze jedno tez w sumie banał ale moze sie przyda Dekorator wnętrz zaproponował by dywan w salonie przykrywał połowę powierzchni prostokątnej podłogi o wymiarach 4,5mx6m brzegi dywanu powinny być jednakowo odległe od ścian salonu Oblicz wymiary dywanu.

Grześ: O jaaa Mateusz jesteś wielki, nie wymyśliłbym lepszych zadań. Masz jeszcze jakieś takie fajne "perełki"

Mateusz: Zobacze jescze do drugiej książki moze cos ciekawego będzie

Mateusz: No nie wiem moze jescze dwa takie 1) Wzdłuż obu dłuższych boków i jednego krótszego boku prostokątnego trawnika o wymiarach 12m na 10m wykopano rabatki kwiatowe o tej samej szerokości.Jaka to szerokość jeśli rabatki

	1
zajmują dokładnie		powierzchni całego trawnika?
	2

2)Na ogrodzenie parkingu w kształcie prostokąta przeznaczono 300 m bieżących siatki.Ozdobna metalowa brama wjazdowa ma mieć szerokość 12m jakie wymiary powinien mieć ten parking aby jego pole powierzchni było największe?Oblicz to pole. Nic więcej ciekawszego z optymalizacji nie mam niestety(reszta to standard jak wszędzie) chyba ze cos na dowodzenie ale nie wiem czy ci sie przyda.

Grześ: Aha, rozumiem. Może te zadania się przydadzą. Z jakich zbiorów je brałeś Nie są na pewno ze zbioru Pazdro

Mateusz: ja brałem je z podręczników

Grześ: aaa, ok Bardzo dziękuję CI za pomoc. Przepiszę sobie treści i może przydadzą się na lekcje

Mateusz: Prosze bardzo. Powodzenia w prowadzeniu lekcji

AS: Sprowokowałeś mnie! Może takie coś? Rozwiązać równanie kwadratowe postaci x² + p*x + q = 0 metodą trygonometryczną. Przypadek 1: Pierwiastki równania mają jednakowe znaki , wtedy q > 0 √Δ = √p² − 4*q = p*√1 − 4q/p²

	4q
Z uwagi na to,że pierwiastki mają być rzeczywiste,wynika.1 −		> 0
	p2

	4q
czyli		< 1
	p2

	4q
Mogę teraz przyjąć,że		= sin2φ
	p2

Pierwiastki szukane

	−p ± √p2 − 4q		−p
x1,2 =		=		(1 ± √1 − 4q/p2)
	2		2

	−p		−p
x1 =		*(1 − cosφ) , x2 =		*(1 + cosφ) lub
	2		2

	2*√q
x1 = −p*sin2(φ/2) , x2 = −p*cos2(φ/2) gdzie sinφ =
	p

Przypadek 2 Pierwiastki równania są różnych znaków czyli q < 0

	−4q		−4q
Liczba		jest dodatnia i możemy przyjąć tgφ =
	p2		p2

	1
Wtedy √Δ = √1 + tg2φ =
	cosφ

Pierwiastki

	−p		1		p		1 − cosφ
x1 =		*(1 −		) =		*
	2		cosφ		2		cosφ

	−p		1		−p		cosφ + 1
x2 =		*(1 +		) =		*
	2		cosφ		2		cosφ

Ostatecznie

	p*sin2(φ/2)
x1 =
	cosφ

	−pcos2(φ/2)		2√−q
x2 =		gdzie tgφ =
	cosφ		p

Przykład Rozwiązać równanie x² − 35.9x + 316.2 = 0

	2*√316.2
sinφ =		= −0.9906
	−35.9

φ = 97^o50' ,φ/2 = 48^o55' x1 = 35.9*sin²48^o55' = 20.4 x2 = 35.9*cos²48^o55' = 15.5

Grześ: Hihi, jak niby Cię sprowokowałem Nie powiem ciekawy sposób rozwiązania równania kwadratowego. Nie wiem, czy takie coś w ogóle warto wyłożyć na lekcji, skoro większość nie rozumie troszkę bardziej skomplikowanych równań kwadratowych i to na tradycyjnych wzorach

Grześ: Jesteś może Mateusz Jakbyś mógł, to powiedz mi do czego odnosi się długość jezdni. Do długości łuku paraboli, czy do długośc tej prostej kreski Bo raczej na lekcji nie przedstawiałbym długośc paraboli z całek...

Grześ: A czy ktoś może mi odpowiedzieć czy dobrze myślę

Godzio: Moja podpowiedź do tego zadania, wrzuć sobie je w układ współrzędnych, gdzie początek jezdni to punkt (0,0) myślę że dalej już sobie poradzisz

Grześ: Dobra, wrzucę sobie w układ, tylko o jedną rzecz mi chodzi, do czego odnosi sie dł. jezdni. Jak sądzisz Godzio

Godzio: Parabola tylko i wyłącznie do jezdni

Grześ: NO właśnie, a skoro mam podaną długość jezdni, czyli paraboli, to co ja z tym mogę zrobić? Tylko o to mi chodzi

Godzio:

	1
108 =		* 2πr ⇒ 2r = ...
	2

2r
	= ... i teraz tylko liczyć wartości w poszczególnych punktach
6

Grześ: aaa, czyli mam przyjąć, że to część łuku okręgu

Godzio: nic innego raczej się nie da

Grześ: hmmm, a dla pewności.... jak kąt wycinka weżmiesz

Grześ: znaczy sie kąt łuku

Godzio: A na co Ci wycinek ?

Godzio: Łuk jest oparty na kącie 180^o więc nie trzeba za dużo kombinować

Grześ: ale w układzie współrzędnych ten wykres inaczej wygląda.... nie jest na 180 stopni. Zapewne nie dało się inaczej krzywej narysować i została narysowana jako półokrąg...

Godzio: poczekaj moment zaraz posprawdzam sobie, może jednak trzeba coś innego wymyśleć

Godzio: wymyślić *

Grześ: widze że jest to ciekawe zadanie, może przyda się na matę Nie musisz mi rozwiązywać, tylko narazie nie wiem dokładnie jak się za nie zabrać

Grześ: wg mnie trzeba wyznaczyć punkt równoodległy od tych 4 wyznaczonych punktów, będzie znajdował się na osi symetrii wykresu. Co o tym sądzisz?

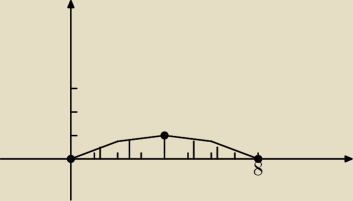
Godzio: Rzeczywiście na pół okrąg to nie wygląda

	1		1		1		1
y = −		x2 +		x = −		x(x − 8) = −		(x − 4)2 + 1
	16		2		16		16

Chyba to tak trzeba:

8		4
	=
6		3

	4
f(		) = ...
	3

	8
f(		) = ...
	3

f(4) = ...

	16
f(		) = ...
	3

	20
f(		) = ...
	3

I to da poprawne wyniki

Grześ: ale teraz trzebaby było wyznaczyć skalę, bo wyniki będą zaniżone od rzeczywistych. Sam pomyśl

Grześ: masz 108 m a tu wyjdą bardzo niskie wyniki....

Grześ: dobra, wyznaczyłem promień tego okręgu. Wynosi 8,5 teraz wg mnie muszę wyznaczyć cięciwę powstałą z osi OX, co o tym sądzisz

Godzio: Mimo to ja bym został przy tym

Godzio: Ale tu z okręgiem to chyba jednak się nie da bo część paraboli raczej nigdy nie będzie okręgiem, wcześniej mnie zmylił rysunek Mateusza i tak jakoś mi się skojarzyło

Grześ: Juz wiem jak policzyć. Kurde bardzo ciekawe zadanie Teraz wyznaczę sobie kąt wycinka, policzę łuk okręgu w tej skali a potem porównam ze skalą rzeczywistego obrazu drogi, hihi

Grześ: Ole ta częśc wykresu jest praktycznie taka sama jak łuk okręgu Nie da się go tak uprościć

Godzio: Nie mam pojęcia

Grześ: sprawdziłem i powstaje tylko lekkie załamanie, Zmiana promienia wynosi z 8,5 na około 8,48, więc jest to praktycznie łuk

Godzio: Ano właśnie, czyli jest obsunięcie co oznacza wynik nie dokładny

Grześ: Ojej, a Twój sposób nie wypali, bo sam pomyśl. Masz długośc osi OX 8, a jezdnia 108 m, jak niby zmieścisz tyle asfaltu

Godzio: 8 jednostek nie metrów więc trzeba coś wymyślić może ten okrąg jest dobrym pomysłem ale jeszcze sobie pomyśle może coś wymyśle

Grześ: taaak, dlatego nie napisałem przy 8 metry Ja tu nie widzę innego pomysłu. Taki błęd mogę się założyć został uwzględniony w rozwiązaniu. Rozumiem, gdyby to był ostry wykres paraboli, wtedy to nie da rady. Ale tu wyznaczony przeze mnie punkt środka okręgu posiada margines błedu w granicach +− 0,02 jednostki

Grześ: Ja idę spać. Jak cos wymyślisz, to pisz.

Godzio: Ok, narazie ale tu chyba nic więcej się nie da

Mateusz: Ojej mogłem sie domyslic ze mogą byc z tym problemy tu chodzi o most taki jak tu np http://pl.wikipedia.org/wiki/Mosty_Warszawskie

Mateusz: Szczególnie patrz na most po lewej ostatnia fotka

Godzio: Czyli można to potraktować jako część okręgu ?

Mateusz: w zadaniu podali nam ze model mostu odzwierciedla parabolka o takim równaniu jak podano w zadaniu rysuje tą parabole w układzie współrzędnych widzimy ze B₃ jest w wierzchołku miejsca zerowe

	108
łatwo policzyc to 0 i 108(punkt B) wiemy ze {AA1|=|AA2|...=|A5B| =		=18 czyli
	6

odległosci między wieszakami wynoszą 18 a więc x=18, 36, 54 itd i teraz liczymy wartosci funkcji(B₁ B₂ itd) dla tych x i dalej juz prosto

Mateusz: Pewnie tak tylko jakbys wtedy wyznaczył wysokosci tych wieszaków

Godzio: Ano dobra, bo w przecież 108 m tyczy się jezdni to znaczy odcinka na OX heh, ale tutaj filozofowaliśmy

Mateusz: w podręczniku w którym mam to zadanie jest obok rysunku fotografia w realu jak ten most wygląda sądziełm ze będzie zbędna a tu prosze jednak okazała sie potrzebna następnym razem pomysle o dodaniu jak będzie potrzeba

Grześ: Hihi, nie mogę jak tu kombinowaliśmy. A wystarczyło określenie czego odnosi się jezdnia i by było po sprawie. Dziękuje za ciekawą polemikę z Godziem

Mateusz: Tak w sumie to tylko z korzyscią dla was z takich polemik mozna się duzo nauczyc i zapamiętać nie wiadomo czy którys z was nie będzie np architektem i nie będzie projektował mostów

AS: Zadania na gimnastykę umysłu 1.Dowieść,że równanie b²x² + (b² + c² − a²)x + c² = 0 nie ma pierwiastków rzeczywistych,jeśli a,b,c oznaczają długości boków trójkąta. 2. Wykazać,że jeżeli a,b,c są miarami boków trójkąta prostokątnego o przeciwprostokątnej c,to równanie x² − 2*(a² + b²)x + c⁴ = 0 ma tylko jeden pierwiastek podwójny. 3. Ile wynosi iloczyn pierwiastków równania dwukwadratowego ax⁴ + bx² + c = 0 w którym b² − 4ac > 0 4. log2*log5 = 0.2104. Obliczyć log2 i log5. 5. Czy równanie kwadratowe zupełne może mieć jako pierwiastki liczby przeciwne?