Wartość bezwzględna!
Aszlej: Doprowadź do najprostszej postaci podane wyrażenie , uwzględniając podane założenie: 1.
|3−x|+|x−1| xnależy (−
∞, 1) Chodzi mi o wytlumaczenie tego typu zadan a nie rozwiązanie

będę
b. wdzięczna

9 gru 18:16
aga116: skoro x∊(−∞,1) to musisz opuscic wartosc bezwzgledna pamietajac o zmianie znakow w odpowiednich
miejscach
9 gru 18:21
Aszlej: no tak, ale w niektórych przypadkach trzeba zmieniać jeszcze to pomiędzy wartościami.

i nie
wiem czemu tak to jest. :..
9 gru 18:23
aga116: ale jakich przypadkach?
tu masz jeden przypadek gdy x∊(−∞, 1)
9 gru 18:25
Aszlej: No tak, taki przykład, ale mi chodzi o to jak mam zmieniać czy "−" zmienia całe wyrazenie? a
"+" nie?
9 gru 18:27
aga116: |3−x| masz takie wyrazenie, podstawiasz sobie w miejsce x dowolne liczby z tego przedzialu (−∞,
1) i patrzysz czy 3 minus ktorakolwiek z tych liczb da wartosc ujemna, jesli nie opuszczasz
wartosc bezwzgledna bez zmiany znakow
9 gru 18:28
aga116: wiec jaki bedzie koncowy rezultat?
9 gru 18:28
nikka: weź dowolną liczbę z przedziału (−∞,1) np. 0 i zobacz jakie wartości mają wyrażenia w modułach
|3−x| = jak podstawisz 0 to otrzymasz 3 czyli wartość jest dodatnia = 3−x
|x−1| = jak podstawisz 0 to otrzymasz −1 czyli wartość jest ujemna = −(x−1)
(powyżej korzystamy z def. wartości bezwzględnej |a| = a dla a ≥ 0 i |a| = −a dla a<0)
|3−x| + |x−1| = 3−x + [−(x−1)] = 3 − x − x + 1 = −2x + 4
9 gru 18:30
Aszlej: aha, a z |x+1| robię to samo?
9 gru 18:30
Szymon : |3(2x−5)−2(4x+1)|=7
30 maj 16:17
Szymon : |3−x|+|x−1|≥2
30 maj 16:19
Szymon : Oblicz mi te 2 działania, będę wdzięczny za to
30 maj 16:20
Mila:
1)
|3(2x−5)−2(4x+1)|=7⇔
|6x−15−8x−2|=7
|−2x−17|=7⇔
|2x+17|=7
2x+17=7 lub 2x+17=−7
dokończ
30 maj 21:20
Mila:
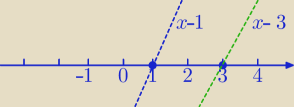
I sposób:
Korzystając z własności wartości bezwzględnej możemy ustalić jaka jest najmniejsza wartość
wyrażenia z lewej strony nierówności:
|3−x|+|x−1|≥|3−x+x−1|=|2|=2
Zatem nierówność jest spełniona dla każdego x∊R
Można się pomęczyć i rozwiązać tak:
2)
|3−x|+|x−1|≥2⇔ ( korzystamy z własności, że |3−x|=|x−3|, to ułatwi trochę)
|x−3|+|x−1|≥2
Na osi zaznaczysz, w jakich przedziałach x−3≥0, x−1≥0 ( x≥3, drugie wyrażenie dla x≥1 )
1)
x<1 ( obydwa wyrażenia są ujemne w tym przedziale)
Mamy nierówność:
−x+3−x+1≥2⇔
−2x+4≥2
−2x≥−2
x≤1 i x<1⇔
x<−1
====
lub
2) x∊<1,3)
−x+3+x−1≥2
2≥2 wszystkie liczby z tego przedziału spełniają nierówność
x∊<1,3)
lub
3)
x≥3
x−3+x−1≥2
2x≥6
x≥3⇔ wszystkie liczby z tego przedziału spełniają nierówność
x≥3
x∊R
30 maj 21:46
 będę
b. wdzięczna
będę
b. wdzięczna
 i nie
wiem czemu tak to jest. :..
i nie
wiem czemu tak to jest. :..
 I sposób:
Korzystając z własności wartości bezwzględnej możemy ustalić jaka jest najmniejsza wartość
wyrażenia z lewej strony nierówności:
|3−x|+|x−1|≥|3−x+x−1|=|2|=2
Zatem nierówność jest spełniona dla każdego x∊R
Można się pomęczyć i rozwiązać tak:
2)
|3−x|+|x−1|≥2⇔ ( korzystamy z własności, że |3−x|=|x−3|, to ułatwi trochę)
|x−3|+|x−1|≥2
Na osi zaznaczysz, w jakich przedziałach x−3≥0, x−1≥0 ( x≥3, drugie wyrażenie dla x≥1 )
1)
x<1 ( obydwa wyrażenia są ujemne w tym przedziale)
Mamy nierówność:
−x+3−x+1≥2⇔
−2x+4≥2
−2x≥−2
x≤1 i x<1⇔
x<−1
====
lub
2) x∊<1,3)
−x+3+x−1≥2
2≥2 wszystkie liczby z tego przedziału spełniają nierówność
x∊<1,3)
lub
3)
x≥3
x−3+x−1≥2
2x≥6
x≥3⇔ wszystkie liczby z tego przedziału spełniają nierówność
x≥3
x∊R
I sposób:
Korzystając z własności wartości bezwzględnej możemy ustalić jaka jest najmniejsza wartość
wyrażenia z lewej strony nierówności:
|3−x|+|x−1|≥|3−x+x−1|=|2|=2
Zatem nierówność jest spełniona dla każdego x∊R
Można się pomęczyć i rozwiązać tak:
2)
|3−x|+|x−1|≥2⇔ ( korzystamy z własności, że |3−x|=|x−3|, to ułatwi trochę)
|x−3|+|x−1|≥2
Na osi zaznaczysz, w jakich przedziałach x−3≥0, x−1≥0 ( x≥3, drugie wyrażenie dla x≥1 )
1)
x<1 ( obydwa wyrażenia są ujemne w tym przedziale)
Mamy nierówność:
−x+3−x+1≥2⇔
−2x+4≥2
−2x≥−2
x≤1 i x<1⇔
x<−1
====
lub
2) x∊<1,3)
−x+3+x−1≥2
2≥2 wszystkie liczby z tego przedziału spełniają nierówność
x∊<1,3)
lub
3)
x≥3
x−3+x−1≥2
2x≥6
x≥3⇔ wszystkie liczby z tego przedziału spełniają nierówność
x≥3
x∊R