Podstawą ostrosłupa jest romb o boku długości a i kącie ostrym 2alfa. Każda ściana boczna jest
nachylona do płaszczyzny podstawy pod kątem beta. Oblicz objętość i pole powierzchni
całkowitej ostrosłupa.
wiem ze w podstawe mozna wpisac okrag..ale to i tak mi nic nie daje. nie umiem tego zrobic
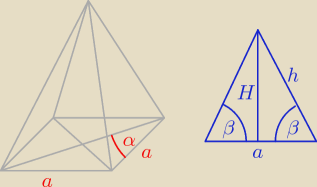h − wysokość ściany bocznej
H − wysokość ostrosłupa
| H | 1 | |||||||||
tgβ = | ⇒ H = | atgβ | ||||||||
| 2 |
| a | |||||||||
cosβ = | ⇒ h = | |||||||||
| h | 2cosβ |
| 1 | 1 | 1 | 1 | |||||
V = | * Pp * H = | * a2*sin2α * | atgβ = | a3 * sin2α * tgβ | ||||
| 3 | 3 | 2 | 6 |
| h * a | a2 | |||
Pc = Pp + Pb = a2*sin2α + 4 * | = a2*sin2α + | |||
| 2 | cosβ |
zapomnialam o tym wzorze 12ab*sinγ
dziękuję Ci serdecznie!