Trójkąt wpisany w trójkąt. Milena: Dane są dwa trójkąty równoramienne: pierwszy o podstawie 3 cm i wysokości opuszczonej na tę podstawę 2 cm oraz drugi o podstawie 5 cm i wysokości opuszczonej na podstawę 4 cm. W trójkąty te wpisano okręgi. Porównaj stosunek obwodów tych trójkątów ze stosunkiem długości wpisanych w nie okręgów. Zadanie niby proste, ale nie potrafię zrobić Proszę o pomoc.

TOmek:

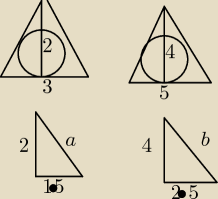
Obw1		r1
	porównać z
obw2		r2

4+2,25=a² a=2,5 16+6,25=b² b=√22,25 czyli mamy juz stosunek obwodów trójkątow

2,5+2,5+3		8
	=
√22,25+√22,25+5		2√22,25+5

−−−−−−−−−−−−−−−− potrzebujemy Pole.. trójkąt po lewej P=6 trójkąt po prawej P=20

	36
rlewy=
	8

	400
rprawy=
	2√22,25+5

bla bla bla... troche dziwny ten bok wyszedł, ale raczej dobrze zrobiłem..

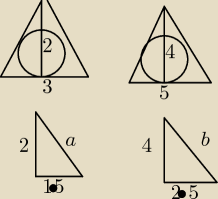
Milena: Dziękuję Ci bardzo Mi właśnie coś podobnego wychodziło, ale w odpowiedziach z tyłu podręcznika jest nieco inaczej: ObwΔ1 : ObwΔ2 = (√89 −5) : 8 a Obw_o1 : Obw_o2 = 3 √89 + 5) : 80