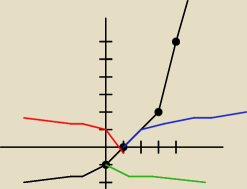
Wykreśl funkcje Osker: (czarny) y=2^x + 2 (czerwony) y=|f(x)| (zielony) y= f(|x|) (niebieski) y=|f(|x|)| Chodzi mi o to czy to jest dobrze narysowane pomijając to że nie ma idealnego kształtu hiperboli =)

think: już w czarnym masz błąd, bo dla x = 0 y = 2⁰ + 2 = 3 no chyba, że we wzorze ma być −2 nie +2

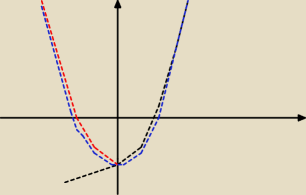
think: zielony jest źle... f(|x|) robię przykład na rysunku jak to wygląda czarna przerywana to f(x) czerwona przerywana to odbicie części czarnego wykresu tej części gdzie x ≥ 0 na drugą stronę. więc niebieska przerywana to f(|x|)

Osker: no tak y=2^x − 2 pomylilem sie ale chodzi mi czy w ten sposob wartosci bezwzgledne sa dobrze wyznaczone

think: przykład liczbowy: f(x) = 2^x − 2 f(|x|) = 2^|x| − 2 f(1) = 2 − 2 = 0 f(|−1|) = 2^|−1| − 2 = 0

think: czyli dla x−ów położonych symetrycznie wartości są te same f(|3|) = f(|−3|) f(|4|) = f(|−4|)

Osker: ok f(|x|) rozumiem a pozostale jak

think: a jak masz źle zielony to automatycznie masz źle niebieski.

think: czerwony jest dobrze...

Osker: myśle mysle i nie wiem jak ten niebieski bedzie

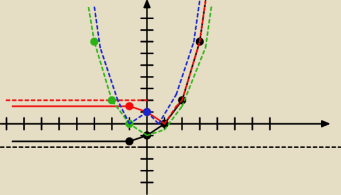
think: oznaczenia kolorystyczne identyczne z Twoimi

Osker: Ok wielkie dzieki