Czy ta nierówność trygonometryczna jest dobrze? bardot: Czy ta nierówność trygonometryczna jest dobrze?

	π		√2		π
sin (x −		) <		; t=x −
	3		2		3

	√2
sint <
	2

	π		3π
t1=		+2kπ ⋁ t2=		+2kπ
	4		4

	7π		13π
x1=		+2kπ ⋁ x2=		+2kπ
	12		12

	−13π		7π
x∊ (		+2kπ ;		+2kπ )
	12		12

M4ciek: Wydaje mi sie ,ze nie mozna tak sobie "t" podstawic.

bardot: zawsze tak robiłem w takich przypadkach i niby wychodziło

M4ciek: To jak odp. sie zgadza to pewnie mozna

Grześ:

	π
zazwyczaj w trygonometrii za wyrażenie x−		powinno powstawiać się α,β...
	3

To po prostu wtedy lepiej wygląda

Grześ: podstawiać*

M4ciek: W sensie z wzoru : sin(α−β) = ....

ArekB: Nie można sobie tak o "t" podstawić, bez założenia, że t do czegoś należy... Bo na razie zrobiłeś funkcję od t, które może być wszystkim...

bardot:

	−11π		7π
no właśnie w odpowiedziach jest: x∊(		+2kπ;		+2kπ)
	12		12

bardot: ok oczywiście t∊<−1;1>

TOMM: Skoro druga liczba się zgadza to w pierwszej może jest błąd rachunkowy, przelicz to jeszcze raz

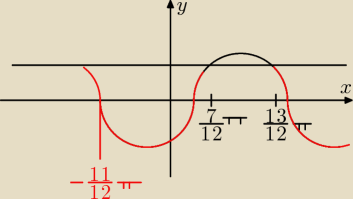
Godzio: W tego typu równaniach nie ma potrzeby robić podstawienia, najpierw rozwiązujemy równanie żeby otrzymać punkty przecięcia:

	π		π		π		3π
x −		=		+ 2kπ lub x −		=		+ 2kπ
	3		4		3		4

	7π		13π
x =		+ 2kπ lub x =		+ 2kπ
	12		12

Teraz szkicujemy sobie wykres,

	13
przesuwamy sobie punkt przecięcia		π o jeden okres do tyłu:
	12

13		11
	π − 2π = −		π
12		12

	11		7
I odpowiedź: x ∊ (−		π + 2kπ,		π + 2kπ)
	12		12

bardot: wielkie dzięki Godziu

Kamyk: czy jest ktoś w stanie mi pomóc?