
 jak H jest podane i hs to możemy obliczyć z twierdzenia Pitagorasa
H2+a2=hs2
242+a2=262
576+a2=676
a2=676−576
a2=100/ pierwiastek
a=10
Pp= a*a=10*10=100
jak H jest podane i hs to możemy obliczyć z twierdzenia Pitagorasa
H2+a2=hs2
242+a2=262
576+a2=676
a2=676−576
a2=100/ pierwiastek
a=10
Pp= a*a=10*10=100
| 1 | ||
V= | *100*24=100*8 ( po skróceniu 3 z 24 ) =800 cm3 | |
| 3 |


 a to zadanie 1 i 4
a to zadanie 1 i 4 
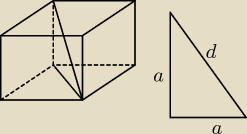 to 1 :
no i z twierdzenia Pitagorasa
a2+a2=d2
2a2=d2/ pierwiastek
√2a2=d / pierwiastek
d= √2a
to 1 :
no i z twierdzenia Pitagorasa
a2+a2=d2
2a2=d2/ pierwiastek
√2a2=d / pierwiastek
d= √2a
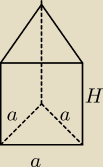 a to 4 ;
H=12
r (różnica) =2
a to 4 ;
H=12
r (różnica) =2



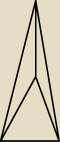 czyli taki
czyli taki
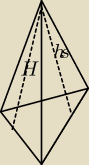

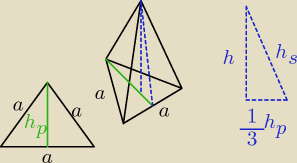 h − wysokość = 24 cm
hs − wysokość ściany bocz = 26 cm
hp wysokość podstawy
13hp = √(hs)2−h2
13hp = √100 = 10
hp = 30 cm
h − wysokość = 24 cm
hs − wysokość ściany bocz = 26 cm
hp wysokość podstawy
13hp = √(hs)2−h2
13hp = √100 = 10
hp = 30 cm
| 2√3*hp | ||
a = | = 20√3 cm
| |
| 3 |
| a*hp | ||
Pp = | = 300√3
| |
| 2 |
| Pp*h | ||
V = | = 300√3*243 = 2400√3 cm3 | |
| 3 |


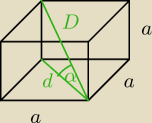 d − przekątna podstawy
D − przekątna sześcianu
a − długość krawędzi
d = a√2
D2 = a2+d2
D = √a2+2a2 = a√3
d − przekątna podstawy
D − przekątna sześcianu
a − długość krawędzi
d = a√2
D2 = a2+d2
D = √a2+2a2 = a√3
| a | √3 | |||
sin α = | = | |||
| D | 3 |
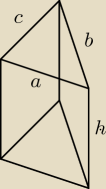 Zad 4
h = 12 najdłuższa krawędź
c = 10 krótsza o r = 12− 2 = 10
b = 8 krótsza o r = 10−2 = 8
a = 6 krótrsza o r = 8−2 = 6
a2 + b2 = c2
62 + 82 = 102
36 + 64 = 100 → z tego wynika,że trójkąt jest prostokątny
Trójkąt prostokątny tw. Pitagorasa
Pp = a*b2 = 6*82 = 24 cm2
V = Pp *h = 24 * 12 = 288 cm3
Pc = 2*Pp + h(a+b+c) = 2*24 + 12(6+8+10) =48 + 48 = 96 cm2
Zad 4
h = 12 najdłuższa krawędź
c = 10 krótsza o r = 12− 2 = 10
b = 8 krótsza o r = 10−2 = 8
a = 6 krótrsza o r = 8−2 = 6
a2 + b2 = c2
62 + 82 = 102
36 + 64 = 100 → z tego wynika,że trójkąt jest prostokątny
Trójkąt prostokątny tw. Pitagorasa
Pp = a*b2 = 6*82 = 24 cm2
V = Pp *h = 24 * 12 = 288 cm3
Pc = 2*Pp + h(a+b+c) = 2*24 + 12(6+8+10) =48 + 48 = 96 cm2