 A = (2, 4), B = (1, 2), C = (−1, 3)
Najpierw trzeba ustalić, które punkty leżą na okręgu oraz który punkt jest punktem przecięcia
stycznych.
S = (x0, y0) to środek okręgu, r − długość promienia okręgu
Wyznaczamy współrzędne punktu P będącego środkiem odcinka łączącego punkty styczności
oraz współczynniki kierunkowe prostych zawierających: punkty S, P i punkt przecięcia stycznych
oraz punkty styczności, te proste są prostopadłe, ich iloczyn jest równy (−1).
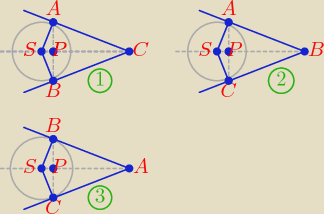
Rozpatrujemy 3 przypadki:
A = (2, 4), B = (1, 2), C = (−1, 3)
Najpierw trzeba ustalić, które punkty leżą na okręgu oraz który punkt jest punktem przecięcia
stycznych.
S = (x0, y0) to środek okręgu, r − długość promienia okręgu
Wyznaczamy współrzędne punktu P będącego środkiem odcinka łączącego punkty styczności
oraz współczynniki kierunkowe prostych zawierających: punkty S, P i punkt przecięcia stycznych
oraz punkty styczności, te proste są prostopadłe, ich iloczyn jest równy (−1).
Rozpatrujemy 3 przypadki:
| 3 | ||
(1): P = ( | , 3), aAB = 2, aPC = 0, 2*0 ≠ −1, ten układ punktów | |
| 2 |
| 1 | 7 | 1 | 1 | |||||
(2): P = ( | , | ), aAC = | , aPB = −3, | *(−3) = −1, | ||||
| 2 | 2 | 3 | 3 |
| 5 | 1 | 3 | 1 | 3 | ||||||
(3): P = (0, | ), aBC = − | , aPA = | , − | * | ≠ −1, | |||||
| 2 | 2 | 4 | 2 | 4 |