PW:
Trzeba wrócić do definicji (pozwolę sobie rozwinąć myśl
AS).
Jest tu głęboka analogia między wektorami a kątami skierowanymi.
Przypomnę, że wektor
→
AB
to według definicji uporządkowana para punktów (pierwszy A, drugi B). I nic więcej, zasadniczo
można by to zapisywać − jak każdą uporządkowaną parę − w postaci (A,B). Przyjęło się, że w tym
szczególnym wypadku rysujemy strzałeczkę, która pokazuje porządek. W napisie nie ma to żadnego
sensu właściwie, jest to pozostałość po rysunku na płaszczyźnie. Narysowanie tylko A i B jako
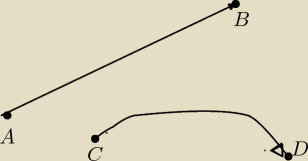
kropek nie daje informacji o porządku, więc rysuje się strzałkę. Można narysować "prostą
strzałkę" jak dla pary (A,B), a można i inną − jak dla pary (C,D) na rysunku. Ważne, żeby
określała kolejność.
Cóż, tradycja jest taka, że rysuje się prostą. W żadnym razie jednak wektor nie jest
"zaostrzonym odcinkiem", to po prostu para punktów.
Identycznie jest z kątem skierowanym.
Definicja jest taka: Kąt skierowany jest to uporządkowana para półprostych o wspólnym początku.
Nie ma tu więc już mowy o kącie jako części wspólnej dwóch półpłaszczyzn, są tylko dwie
półproste i porządek, który zaznaczamy strzałką. Znowu nie jest ważne, jak narysujemy tę
strzałkę, ważne żeby określała porządek półprostych.
Następna analogia: Jak się dodaje wektory? Musi być tak, że początek drugiego jest końcem
pierwszego, czyli umiemy dodawać tak: (A,B)+(B.D)=(A,D) − a jeżeli jest inaczej, to jeden z
wektorów przesuwamy. Wynika stąd, że jeśli dodamy (A,B)+(B,A)=(A,A), to dostaniemy wektor, w
którym początek i koniec pokrywają się, a taki wektor jest "wektorem zerowym" − dodawanie go
do dowolnego wektora (X,Y) daje (X,Y). Dlatego mówimy, że wektorem przeciwnym do (A,B) jest
(B,A) − bo w sumie dają wektor zerowy. Tak samo jest dla kątów skierowanych, jak to
przypomniał
AS − kąt skierowany przeciwny to para tych samych półprostych o odwrotnym
porządku (bo ich suma jest "kątem zerowym" − są to dwie pokrywające się półproste).
Natura ludzka jest taka, że człowiek chce mierzyć i opisywać, dlatego wprowadza się pojęcie
długości wektora (ale to nie mówi wszystkiego o wektorze, więc jeszcze kierunek i zwrot).
Podobnie dla kąta skierowanego: wprowadza się pojęcie miary tego kąta (ale to nie mówi
wszystkiego, więc jeszcze orientacja, kierunek obrotu). Jeżeli mówimy o kącie zorientowanym
110°, to mamy na myśli kąt dodatnio zorientowany (trzeba zajrzeć do książki − co to znaczy
dodatnio i jak to się mierzy, bo dwie półproste wyznaczają dwa kąty na płaszczyźnie). Kąt do
niego przeciwny to kąt o odwrotnym porządku półprostych.
Rozpisałem się może niepotrzebnie, ale chcę zwrócić uwagę, jak pewne rzeczy pozornie odległe i
wydające się trudne stają się oczywiste po zrozumieniu struktury − i nie trzeba się ich uczyć
"osobno".
A − kąt skierowany dodatni
B − kąt skierowany przeciwny