Styczne do okręgu Alberttynka iZenek: Udowodnij,że cięciwa d łącząca punkty styczności stycznych do okręgu K(O;r) przechodzących przez punkt A ma długość :

	2r
d=		(|AO|2 − r2)0,5
	|AO|

b) dla jakich wartości stosunku ^r_|AO| punkty A,O i punkty styczności tworzą kwadrat

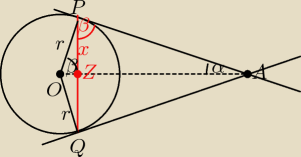
think: |AP|² = |OA|² − r² trójkąty AZP, OZP i OPA są podobne

|AP|		|OA|
	=		⇒ x = ...
x		r

d = 2x

think: co do podpunktu b, to musisz zauważyć, że r odpowiada długości boku kwadratu, a odległość przeciwległych wierzchołków to....

Alberttynka iZenek: d=2x(?!)− na "optykę"

Jack: bo trójkąty ZPA i ZQA są przystające

Alberttynka iZenek: Przystające na konkretnym rysunku ?

Jack: włóż trochę wysiłku i udowodnij to jeśli nie jest to dla Ciebie jasne.

Zygmunt: Myślę po prostu,że gdy powiemy,iż trójkąty OPA i OAQ są identyczne jak dwie siostry,to x=h,i to wyjaśnia sprawę!