zaznacz na osi liczbowej liczby spełniajace podane warunki
merek: Ix−3I=2 i IxI=1
Ix+2I<5 i Ix−1I≥2
5 gru 13:07
brg: musisz nzaleźć kolejno
a) x odlegle od liczby 3 o równo 2
b) iksy odlegle od liczby −2 o mniej niż 5
c). iksy odlegle od 1 o co najmniej 2 (czyli wiecej niż 2 z dwojką włącznie
Narysuj i napisz co wyszło
5 gru 13:16
brg: opościlem przyklad b) mozna potraktowac to jako |x−0|=1
czyli znajdujesz iksy w ukladze współrzędnych odległe równo 1 od liczby 0.
5 gru 13:20
klkl: x ≥ −4
3 paź 20:40
Gustlik:
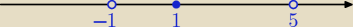
Ix−3I=2
x=3±2⇔x=5 v x=1
IxI=1
x=1 v x=−1
Spójnik "i" oznacza część wspólną zbiorów rozwiązań obu równań, czyli x=1.
4 paź 02:06
Gustlik:
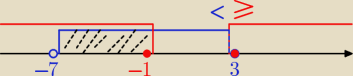 Ix+2I<5
Ix+2I<5 i
Ix−1I≥2
Ix+2I<5
x=−2±5⇔x=3 v x=−7
x∊(−7, 3)
Ix−1I≥2
x=1±2⇔x=3 v x=−1
x∊(−∞, −1>U<3, +∞)
Odp: x∊(−7, −1>
4 paź 02:14
ania: d={xcR IxI>5}
21 lis 11:22
Aga1.: To też jest z matury?
21 lis 12:04
Artur_z_miasta_Neptuna:
Aguś ... raczej nie −−− patrz na daty

21 lis 12:05
Aga1.: Patrzę i widzę 21.11.godz. 11:22
21 lis 12:17
nick1: |x+2||=3
17 gru 20:04
Miso: jkππjkjkjkkkkkk∞ΩΩΩΩΩ
17 wrz 14:41
Miso:
17 wrz 14:42
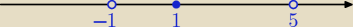 Ix−3I=2
x=3±2⇔x=5 v x=1
IxI=1
x=1 v x=−1
Spójnik "i" oznacza część wspólną zbiorów rozwiązań obu równań, czyli x=1.
Ix−3I=2
x=3±2⇔x=5 v x=1
IxI=1
x=1 v x=−1
Spójnik "i" oznacza część wspólną zbiorów rozwiązań obu równań, czyli x=1.
 Ix+2I<5 i Ix−1I≥2
Ix+2I<5
x=−2±5⇔x=3 v x=−7
x∊(−7, 3)
Ix−1I≥2
x=1±2⇔x=3 v x=−1
x∊(−∞, −1>U<3, +∞)
Odp: x∊(−7, −1>
Ix+2I<5 i Ix−1I≥2
Ix+2I<5
x=−2±5⇔x=3 v x=−7
x∊(−7, 3)
Ix−1I≥2
x=1±2⇔x=3 v x=−1
x∊(−∞, −1>U<3, +∞)
Odp: x∊(−7, −1>
