trygonometria dario: zad1: oblicz cosinus kąta jaki tworzy przekatna sześcinu z podstawą. zad2:w okrąg o promieniu 3 wpisano trójkąt tak,że jeden z boków trójkata jest średnica okregu.

	2
sinus jednego z katów ostrych tego tr. jest równy		. oblicz pole tego tr.
	3

	1−cosx)(1+cosx)
zad3;		=0,4 rozwiąż równanie
	sinx*cosx

	√3+sinx
zad4; znajdz miarę kąta ostrego dla którego jest spełniony warunek		=cosx+1
	√3

prosze o pomoc

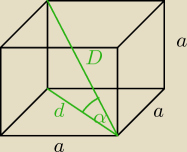dero2005: 2a² d² d = a√2 D² = a² + d² = a² +2a² = 2a² D = a√3 cos α = ^d_D = ^a√2_a√3 = ^√6₃

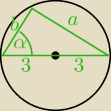dero2005: ^a₆ = sin α =²₃ a = 4 b² + 4² = 6² b = 2√5

dero2005:

(1−cosx)(1+cosx)
	= 0,4 sinx≠0 cosx≠0 x≠0+kπ x≠π2+kπ
sinx*cosx

12−cos2x
	= 0,4
sinx*cosx

sin2x
	= 0,4
sinx*cosx

sinx
	= 0,4
cosx

tgx = 0,4 x = arctg 0,4 = 21°48'

dero2005:

√3+sinx
	= cosx+1
√3

√3+sinx = √3(cosx+1) √3+sinx = √3cosx + √3 sinx = √3cosx ^sinx_cosx = √3 tgx = √3 x = 60°