pomoc ilak: okrąg o równaniu x² − 6x +y² − 2y +2 = 0 i prosta o równaniu x+3y+2=0 przecinaja sie w punktach A,B. Wyznacz długosc cięciwy AB tego okregu. x²+y² − 2ax−2by +c=0 c=a² +b² −r² c=40 −r² jak to zrobic?

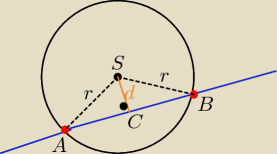
Eta: 1/ sposób: rozwiąż układ równań tej prostej z danym okręgiem otrzymarz współrzędne punktów A i B i wyznacz |AB|=....... 2/ sposób , jak na rysunku

	−6		−2
S(		,		) = ( 3, 1) r2= 32 +12 −2= 8 to r= 2√2
	−2		−2

odległość d punktu S(3,1) od cięciwy: x+3y+2=0

	| 3*1 +1*3+2|		8
d=		=
	√32+12		√10

z trójkąta ACS z tw. Pitagorasa: |AC|² = r² −d²

	64
|AC|2= 8 −
	10

|AC| =...... |AB|= 2*|AC|= ..............

ilak: a mogłabys mi powiedziec ten 1 sposób?− z czego mam zrobic układ równan>

Gustlik: Obliczam środek i promien okręgu: x²+y²+Ax+By+C=0 x² − 6x +y² − 2y +2 = 0 x² + y²− 6x − 2y +2 = 0

	A		−6
a=−		=−		=3
	2		2

	B		−2
b=−		=−		=1
	2		2

r=√a²+b²−C=√3²+1²−2=√9+1−2=√8=2√2 Środek S=(3, 1), promień r=2√2 Obliczam odległość środka okręgu od prostej zawierającej cięciwę x+3y+2=0:

	|Ax0+By0+C|
d=
	√A2+B2

	|3+3*1+2|		|8|		8√10		4√10
d=		=		=		=
	√12+32		√10		10		5

Oznaczam sobie przez x połowę cięciwy, wówczas promień r, odległość środka okręgu od cięciwy d oraz połowa cięciwy x utworzą trójkat prostokątny, gdzie d i x będą przyprostokątnymi, a r przeciwprostokątną. Z twierdzenia Pitagorasa mamy: r²=d²+x²

	4√10
(√8)2=(		)2+x2
	5

	16*10
8=		+x2
	25

	160
8−		=x2
	25

200		160
	−		=x2
25		25

40
	=x2 /√
25

	√40
x=
	5

	2√10
x=
	5

	2√10		4√10
Cięciwa = 2x=2*		=
	5		5

Eta: A co innego ja podałam Gustliku No chyba,że z nudów chciałeś soie popisać