Hiperbola
Maniek:
| | 3 | |
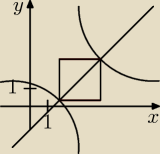
Hiperbola na rysunku jest wykresem funkcji y = |
| + 2 |
| | x−4 | |
Zaznaczona prosta jest osią symetrii tego wykresu. Oblicz Pole kwadratu.
Korzystałem ze wzoru na odległość 2 punktów od siebie ale cos nie wychodziło
. Będę bardzo
wdzięczny za rozwiązanie
4 gru 23:30
Godzio:
A coś więcej masz ? równanie tej prostej ? punkty przecięcia ? Czy tą prostą też trzeba znaleźć
?
4 gru 23:39
Maniek: Nic więcej w poleceniu nie ma
4 gru 23:40
Godzio:
Umiesz obliczyć wzór tej prostej ?
4 gru 23:41
Maniek: tak
4 gru 23:44
think: ta odległość to odległość między wierzchołkami hiperbol
| | 3 | |
x = |
| ⇒ x = √3 = y lub x = −√3 = y |
| | x | |
czyli przekątna kwadratu to długość odcinka między punktami (−
√3, −
√3) a (
√3,
√3)
d =
√(√3 + √3)2 + (√3 + √3)2 =
√24
bok kwadratu to a = U{d}{
√2 =
√12
pole kwadratu a
2 = 12
4 gru 23:46
Godzio:
To w takim razie w czym problem ?
− wyznaczasz prostą
− przyrównujesz równanie prostej do równania hiperboli otrzymując punkty których odległość jest
a√2 gdzie a to bok kwadratu i z tego wyznaczasz "a" i liczysz pole
4 gru 23:47
think: chyba jesteś zmęczony, wrzucasz dzisiaj mnóstwo zadań tego typu a nie wyciągasz żadnych
wniosków z rozwiązań jakie otrzymujesz...
4 gru 23:48
Eta:
Zatem mam z głowy ........ dzięki wybawcy
thinkuś i
Godzio
4 gru 23:51
Maniek: Właśnie pierwsza reakcja jak spojrzałem na zadanie to o ale proste. A teraz jak patrze na twoje
rozwiązanie to nie rozumie dlaczego te punkty to (−√3, −√3) a (√3, √3) a nie (4 + √3, 2 +
√3) i (4 − √3, 2 − √3)
4 gru 23:55
Godzio:
A mi się udało cudem wejść ... komp mi coś nawala
4 gru 23:55
think: Maniek, bo zignorowałam przesunięcie o wektor gdyż nie zmienia ono odległości
4 gru 23:58
Maniek: aha faktycznie zmeczony jestem chyba
teraz wiem o co chodzi, ale dlaczego d = √(√3 + √3)2 +
(√3 + √3)2 = √24 w nawiasach są same
√3 ?
5 gru 00:02
5 gru 00:03
Maniek: ludzie złoci chyba jedna kawa to za mało wybaczcie
5 gru 00:05
think: ponieważ wzór na odległość dwóch punktów:
A = (xa, ya) i B = (xb, yb)
|AB| = √(xb − xa)2 + (yb − ya)2
teraz gdy masz punkty (−√3; −√3) i (√3; √3)
d = √(√3 − (−√3))2 + (√3 − (−√3))2 = √(√3 + √3)2 + (√3 + √3)2 które
napisałam...
5 gru 00:06
think: Maniek zamiast się szprycować kawą to się wyśpij jak człowiek i pracuj nad tymi zadaniami o
jakiejś przyzwoitszej porze
5 gru 00:07
5 gru 00:09