Hiperbola Maniek: Znajdź równania prostych które są osiami symetrii hiperboli:

	−5
a) y =		+ 2
	x

Zrobiłem i wyszło mi y = −x + 2, a w odpowiedziach dodatkowo jest jeszcze y = x + 2. Dlaczego ?

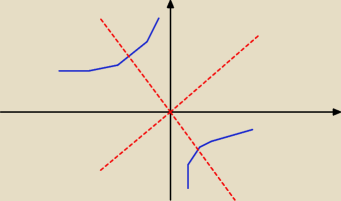
Eta: hiperbola ma dwie osie symetrii sorry za koślawy rysunek

Maniek: Dzięki bardzo mam dla ciebie ostatnie zadanie był bym wdzieczny za rozwiązanie

Maniek: Kurcze tak przekształcam ten wzór a i tak mi nie wychodzi może ktoś rozwiązać to zadanie ? Albo chociaż wypisać wierzchołki

think: a co Ci nie wychodzi?

Godzio: Każda hiperbola ma 2 osie symetrii y = x i y = −x jeśli przesuwasz hiperbolę o jakiś wektor w tym wypadku [0,2] to te proste także zostają przesunięte o ten wektor, więc otrzymujemy: y = x + 2 i y = −x + 2

think: w tym zadaniu wierzchołki paraboli leżą na prostej y = −x liczysz te wierzchołki i jedna prosta symetrii przechodzi właśnie przez oba te wierzchołki natomiast druga oś symetrii jest prostopadła do tej pierwszej i przechodzi przez punkt, który stanowi środek odległości między jednym wierzchołkiem paraboli a drugim. wzór na środek odcinka A = (x_a; y_a) B = (x_b; y_b)

|AB|		xa + xb		ya + yb
	= (		;		)
2		2		2