Zastosowanie całki oznaczonej student2gr1: Witam Mam do policzenia zadania z całki oznaczonej a nie wiem jak się za nie zabrać. Całkowanie nie jest moją mocną stroną Zadanie 1. Obliczyć pole figury ograniczonej krzywą y²=x²−x⁴ Zadanie 2. Obliczyć pole figury ograniczonej krzywymi y²−x+1=0 i x−2y−4=0 Chciałbym prosić nie tylko o wynik ale o krótki opis zadania jak można podobne przykłady wyliczyć. Pozdrawiam

sushi_ gg6397228: najpierw zrob rysunek, pole figury pod wykresem to bedzie calka po przedziale...

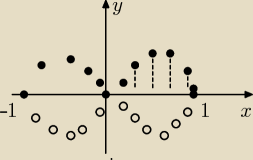AS: Pole obszaru zawartego między osią Ox a wykresem krzywej y = f(x) w przedziale <a,b> oblicza się wzorem b P = ∫f(x)dx a W naszym zadaniu f(x) = x*√1 − x² dla górnej części i f(x) = −x*√1 − x² dla dolnej części Wyliczam pole jednej części (tej zakreskowanej) w przedziale <0,1> Całka nieoznaczona J = ∫x*√1 − x²dx

	−1
Podstawienie: 1 − x2 = t −2xdx = dt ⇒ xdx =		dt
	2

	−1		−1		−1		−1
J =		*∫√tdt =		*∫t1/2dt =		*t3'2/(3/2) =		*t*√t
	2		2		2		3

	−1
J =		*(1 − x2)*√1 − x2
	3

Obliczam pole jednego obszaru (zakreskowanego)

	−1
P1 =		*(1 − x2)*√1 − x2 | [1,0]
	3

−1		−1
	*(1 − 12)*√1 − 12 −		*(1 − 02)*√1 − 02 = 0 + 1/3 = 1/3
3		3

Pole obszaru nad osią Ox wynosi 2*(1/3) = 2/3 a po dodaniu obszaru pod osią Ox 4/3

Alberttynka: Zad 2 Najpierw wyróżnij następujące punkty(ułatwiające podział na obszary normalne−których pola łatwo policzyć i zsumować) P₁(wierzchołek paraboli y²=x−1) −P₁(1;0) P₂ i P₃ − y²−x+1=0 ⋀ x−2y−4=0 ; P₁(2;−1) ; P₂(10;3) P₄;x−2y−4=0 ⋀ y=0 ₄(4;0) Teraz sumuj(najlepiej patrząc na rysunek) 10 2 ∫√x−1dx +∫√x−1dx +(4−2)(0+1)(0,5) −(10−4)(3−0)(0,5) =? 1 1 [ ³²₃ ]

AS: Szukane pole składa się z pól czterech obszarów Równanie krzywej f(x) = √x − 1 położonej nad osią Ox i równanie krzywej f(x) = −√x − 1 położonej pod osią Ox Obliczam całkę nieoznaczoną J = ∫√x − 1dx podstawienie x − 1 = t ⇒ dx = dt J = ∫√tdt = ∫t^1/2dt = 2/3*t^2/3 = 2/3*(x − 1)*√x − 1 Pole 1−ego obszaru − pod górną krzywą w <1,10> P1 = 2/3*(x − 1)*√x − 1 [1,10] = 2/3*(10 − 1)*√10 − 1 − 0 = 18 Pole 2−ego obszaru (trójkąta) w <4,10> P2 = 1/2*(10 − 4)*3 = 9 Pole 3−go obszaru − pod osią Ox P3 = −2/3*(x − 1)*√x − 1[1,2] = −2/3*1*1 − 0 = −2/3 Pole 4−ego obszaru − trójkąta pod osią Ox P4 = 1/2*(4 − 2)*(−1) = −1 Szukane pole P = P1 − P2 + |P3| + |P4| = 18 − 9 + 1 + 2/3 = 32/3