Eta:
1
o −−−− rozkładamy lewą stronę na czynniki
2
o −−− wyznaczamy miejsca zerowe
3
o −−− rysujemy "falę " przez te miejsca ( jezeli pierwiastki są parzyscie krotne
to "fala" w tych miejscach zerowych odbija od osi i nie przechodzi nad oś
( poczytaj o tym na stronie
Jakuba w podanym linku
"falę " rysujemy od prawej strony
od góry jezeli współczynnik przy najwyższej
potędze "x" jest dodatni
a
od prawej od dołu jeżeli współczynnik przy najwyższej potędze "x" jest ujemny
4
o −−− odczytujemy odpowiednie wartości ( w zależności od zwrotu nierówności)
podam rozwiązanie
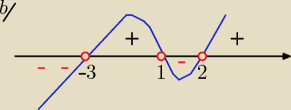
b) x
3 −x −6x +6≤0
x( x
2 −1) −6( x−1) ≤0
x( x−1)(x+1) −6(x−1)≤0
( x−1) *[x(x+1)−6]≤0
( x−1)( x
2+x −6)≤0
x= 1 v x
2+x −6=0 −−−−− liczysz deltę i x
1 x
2
otrzymasz x= 1 v x
1= 2 v x
2 = −3
teraz z rys. wybierasz wartości <0
odp: x€ ( −∞, −3) U (1, 2)
pozostałe podobnie
Eta:
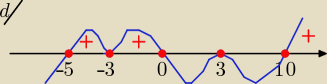
to jeszcze przykład
d) −x
2+9= 9−x
2= ( 3−x)(3+x)
masz tu gotowy rozkład na czynniki
x( (3−x)
2 ( 3+x)
2( x−10)(x +5) ≥0
x=0
x= 3 −− pierw. dwukrotny ( wykres odbije w tym punkcie)
x= −3 −−− też dwukrotny ( wykres też odbije)
x= 10
x= −5
i rysujemy "falę" ( od prawej od góry)
bo +x*(+x
2)*(+x
2) *(+x)*(+x) >0
odp: x€ < −5, 0> U < 10, ∞) przedziały domknięte , bo nierówność
≥0
teraz spróbuj sama pozostałe
Ja już niestety idę do spania ,bo padam
Powodzenia , dobranoc