Poradaa, wielomiany
arigatou: Witam. Miałbym pytanie odnośnie grupowania wielomianów. Jak należy grupować wielomiany tego
typu:
x
4−8x
3+14x
2−13x+6>0, jakimś innym sposobem niż znalezieniem pierwiastka wielomianu z
Bezouta?
Wiele osób umie grupować je wyszukując prawdopodobne ''wspolne nawiasy'', czy jest na to jakiś
sposób, czy to się rzuca jakoś w oczy? Jak tak to prosiłbym o wyjaśnienie, bo przydała by się
ta umiejętność

Bo liczenie z Bezouta też jest czasochłonne. Pozdrawiam
3 gru 18:50
arigatou: ma ktoś jakieś porady?

Z pewnością ktoś tutaj ma upatrzony sposób
3 gru 19:23
arigatou: ponawiam... ważne

albo proszę chociaż o rozwiązanie przykładu
x
4−8x
3+14x
2−13x+6>0
(x
3−7x
2+7x−6)(x−1)
z Bezouta widać, że podzielny jest przez (x−1)
x
3−7x
2+7x−6
____________
x
4−8x
3+14x
2−13x+6

x−1)
−x
4+x
3
_______
−7x
3+14x
2−13x+6
7x
3−7x
2
________
7x
2−13x+6
−7x
2+7x
________
−6x+6
6x−6
___
==
Jak to dalej rozbić?
5 gru 11:38
Petrus: Wydaje mi się, że tu nie pogrupujesz wyrazów. Musisz znaleźć pierwiastki całkowite i wymierne,
a następnie umieścić je w nawiasach
5 gru 11:43
arigatou: czyli? Mógłbyś to przedstawić?

5 gru 11:49
mac:
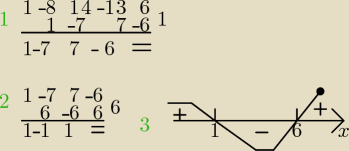
D
6 = {−1,1,−2,2,−3,3,−6,6}
W(x) = x
4 − 8x
3 + 14x
2 − 13x + 6
W(−1) = 1 + 8 + 14 + 13 + 6 ≠ 0
W(1) = 1 − 8 + 14 − 13 + 6 = 0
I teraz najłatwiej schematem Hornera(1). − powyżej
No i teraz masz formę:
(x
3 −7x
2 + 7x − 6)(x−1)>0
No i znowu dzielniki:
D
−6={−1,1,−2,2,−3,3,−6,6}
W(x) = x
3 − 7x
2 + 7x − 6
W(−1) = −1 − 7 − 7 −6 ≠ 0
W(1) = 1 − 7 + 7 −6 ≠ 0
W(−2) = −8 − 28 − 14 − 6 ≠ 0
W(2) = 8 − 28 + 14 − 6 ≠ 0
W(−3) = −27 −63 − 21 − 6 ≠ 0
W(3) = 27 − 63 + 21 − 6 ≠ 0
W(−6) = −216 − 252 − 42 − 6 ≠ 0
W(6) = 216 − 252 + 42 − 6 = 0
Czyli tak samo jak w poprzednim : Hornerem (2)
Czyli po dzieleniu mamy:
(x
2 −x + 1)(x − 6)(x − 1)>0
Δ = 1 − 4 = −3 < 0 czyli ∅
Czyli nierówność: (3)
odp: x∊(−
∞;1)U(6;+
∞)
Sprawdź sam/a, Chyba się nigdzie nie pomyliłem chociaż mam tendencje do zmiany znaków przez co
wynik wychodzi zły

.
5 gru 12:05
arigatou: dzięki^^ tak właśnie to robiłem

5 gru 13:01
 Bo liczenie z Bezouta też jest czasochłonne. Pozdrawiam
Bo liczenie z Bezouta też jest czasochłonne. Pozdrawiam
 Z pewnością ktoś tutaj ma upatrzony sposób
Z pewnością ktoś tutaj ma upatrzony sposób
 albo proszę chociaż o rozwiązanie przykładu
x4−8x3+14x2−13x+6>0
(x3−7x2+7x−6)(x−1)
z Bezouta widać, że podzielny jest przez (x−1)
x3−7x2+7x−6
____________
x4−8x3+14x2−13x+6
albo proszę chociaż o rozwiązanie przykładu
x4−8x3+14x2−13x+6>0
(x3−7x2+7x−6)(x−1)
z Bezouta widać, że podzielny jest przez (x−1)
x3−7x2+7x−6
____________
x4−8x3+14x2−13x+6 x−1)
−x4+x3
_______
−7x3+14x2−13x+6
7x3−7x2
________
7x2−13x+6
−7x2+7x
________
−6x+6
6x−6
___
==
Jak to dalej rozbić?
x−1)
−x4+x3
_______
−7x3+14x2−13x+6
7x3−7x2
________
7x2−13x+6
−7x2+7x
________
−6x+6
6x−6
___
==
Jak to dalej rozbić?

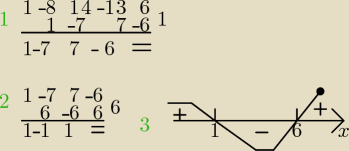 D6 = {−1,1,−2,2,−3,3,−6,6}
W(x) = x4 − 8x3 + 14x2 − 13x + 6
W(−1) = 1 + 8 + 14 + 13 + 6 ≠ 0
W(1) = 1 − 8 + 14 − 13 + 6 = 0
I teraz najłatwiej schematem Hornera(1). − powyżej
No i teraz masz formę:
(x3 −7x2 + 7x − 6)(x−1)>0
No i znowu dzielniki:
D−6={−1,1,−2,2,−3,3,−6,6}
W(x) = x3 − 7x2 + 7x − 6
W(−1) = −1 − 7 − 7 −6 ≠ 0
W(1) = 1 − 7 + 7 −6 ≠ 0
W(−2) = −8 − 28 − 14 − 6 ≠ 0
W(2) = 8 − 28 + 14 − 6 ≠ 0
W(−3) = −27 −63 − 21 − 6 ≠ 0
W(3) = 27 − 63 + 21 − 6 ≠ 0
W(−6) = −216 − 252 − 42 − 6 ≠ 0
W(6) = 216 − 252 + 42 − 6 = 0
Czyli tak samo jak w poprzednim : Hornerem (2)
Czyli po dzieleniu mamy:
(x2 −x + 1)(x − 6)(x − 1)>0
Δ = 1 − 4 = −3 < 0 czyli ∅
Czyli nierówność: (3)
odp: x∊(−∞;1)U(6;+∞)
Sprawdź sam/a, Chyba się nigdzie nie pomyliłem chociaż mam tendencje do zmiany znaków przez co
wynik wychodzi zły
D6 = {−1,1,−2,2,−3,3,−6,6}
W(x) = x4 − 8x3 + 14x2 − 13x + 6
W(−1) = 1 + 8 + 14 + 13 + 6 ≠ 0
W(1) = 1 − 8 + 14 − 13 + 6 = 0
I teraz najłatwiej schematem Hornera(1). − powyżej
No i teraz masz formę:
(x3 −7x2 + 7x − 6)(x−1)>0
No i znowu dzielniki:
D−6={−1,1,−2,2,−3,3,−6,6}
W(x) = x3 − 7x2 + 7x − 6
W(−1) = −1 − 7 − 7 −6 ≠ 0
W(1) = 1 − 7 + 7 −6 ≠ 0
W(−2) = −8 − 28 − 14 − 6 ≠ 0
W(2) = 8 − 28 + 14 − 6 ≠ 0
W(−3) = −27 −63 − 21 − 6 ≠ 0
W(3) = 27 − 63 + 21 − 6 ≠ 0
W(−6) = −216 − 252 − 42 − 6 ≠ 0
W(6) = 216 − 252 + 42 − 6 = 0
Czyli tak samo jak w poprzednim : Hornerem (2)
Czyli po dzieleniu mamy:
(x2 −x + 1)(x − 6)(x − 1)>0
Δ = 1 − 4 = −3 < 0 czyli ∅
Czyli nierówność: (3)
odp: x∊(−∞;1)U(6;+∞)
Sprawdź sam/a, Chyba się nigdzie nie pomyliłem chociaż mam tendencje do zmiany znaków przez co
wynik wychodzi zły  .
.
