Bryły obrotowe BlaBlaBa: Prooooszę Trójkąt prostokątny o przyprostokątnych długości 6cm i 8cm obraca się dookoła przeciwprostokątnej. Oblicz objętość i pole pow całkowitej powstałej bryły.

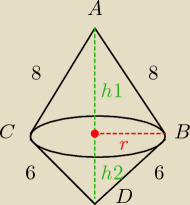a: x − długość przeciwprostokątnej Długość przeciwprostokątnej obliczamy z twierdzenia Pitagorasa: 6² + 8² = x² 36 + 64 = x² x = 10 [cm] W wyniku obrotu trójkąta prostokątnego wokół przeciwprostokątnej powstanie bryła, składająca się z dwóch stożków, mających tę samą podstawę. (patrz rysunek) Objętość tej bryły będzie sumą objętości obu stożków

	1
Vstożka1 =		* πr2 * h1
	3

	1
Vstożka2 =		* πr2 * h2
	3

	1		1		1
Vbryły =		* πr2 * h1 +		* πr2 * h2 =		* πr2(h1 + h2)
	3		3		3

h₁ + h₂ = 10 (długość przeciwprostokątnej) Zauważ, że promień jest jednocześnie wysokością trójkąta ABC. Pole tego trójkąta, jako że jest

	8 * 6
prostokątny, wynosi:		= 24
	2

10r
	= 24
2

10r = 48

	24
r =
	5

Mamy wyliczone promień i wysokość, zatem możemy obliczać objętość

	1		576π		192π		384π
Vbryły =		*		* 10 =		* 10 =		= 76, 8 π [cm3]
	3		25		25		5

Pole powierzchni całkowitej będzie sumą pól powierzchni bocznych obu stożków

	24π
Ppbocznej1 =		* 8 = 38, 4π [cm2]
	5

	24π
Ppbocznej2 =		* 6 = 28, 8π [cm2]
	5

P_pcałkowite = 38, 4 + 28, 8 = 67, 2π [cm²]

BlaBlaBa: O raaaany! Dzięki wielkie

amator: gdzieś musiałeś mieć błąd bo odpowiedź w książce objętość wynosi 96 π cm³

Aga1.:

1		1
	*10*r=		*6*8
2		2

r=4,8

	1
V=		*π*(4,8)2*10=76,8 −−jest to prawidłowa odp.
	3

Nick: Trójkąt prostokątny o przyprostokotnych długości 5cm i 12cm obtaczamy wokół dłuższej przyprostokątnej oblicz objętość i pole powierzchni bocznej powstałej bryły

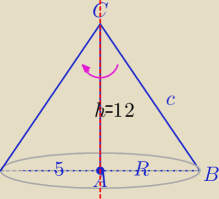Mila: c²=12²+5² c²=169 c=13 l=c=13

	1		1
V=		*π*R2*h=		*π*52*12
	3		3

V=100π [j³] P_b=π*r*l=π*5*13 P_b=65π [j²] ==================