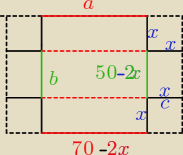
Zadanie optymalizacyjne Ewelina : Z prostokątnego arkusza kartonu o wymiarach 50cm na 70 cm wycinamy z narożnika cztery jednakowe kwadraty. Z pozostałych części kartonu sklejamy otwarte prostopadłościenne pudło. Wyznacz wymiary pudełka, tak aby pole jego powierzchni bocznej było największe. Doszłam do Pp=−8x+240x i nie wiem co dalej. Czy mógłby ktoś mi pomóc?

Eta: wymiary pudełka a= 70 −2x , b= 50 −2x c= x , x >0 P_b = 2ca + 2cb P_b(x) =2x(70−2x) + 2x( 50−2x) = −4x² +240x −−−− f. kwadratowa ramiona paraboli do dołu zatem osiąga maximum dla x_w

	−b
xw= xmax=		= 15
	2a

podaj teraz wymiary maxym. tego pudełka a=.... b=..... c= ..... P_b ( max) = −415²+240*15= 1 800 cm² po wyznaczeniu a,b,c, −−−− możesz sprawdzić max. wartość pola bocznego

klaudia: powinno być Pb(x)= −8x² + 240 x