geometria, proszę o pomoc
corn: Na zewnatrz trzech bokow trojkąta prostokatnego rownoramiennego o przyprostokatnej dlugosci b
zbudowano kwadraty. Srodki tych kwadratow polaczono odcinkami. Oblicz pole otrzymanego
trojkata KLM, gdzie K,L,M są srodkami kwadratow zbudowanych odpowiednio na bokach AC, BC i AB
30 lis 15:08
Godzio:
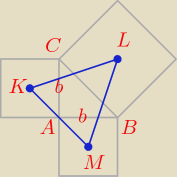
h −− wysokość trójkąta ABC
|KM| = x
|LA| = H
x = b
√2 (2 * połowa przekątnej kwadratu o boku b)
| | 1 | | 1 | | 1 | |
PABC = |
| b2 = |
| *h*b√2 ⇒ h = |
| b√2 |
| | 2 | | 2 | | 2 | |
| | 1 | | 1 | |
H = h + |
| |CB| = |
| b√2 + b√2 = 1,5 * b√2 |
| | 2 | | 2 | |
| | 1 | | 1 | | 3 | |
PKLM = |
| H*x = |
| * b√2 * 1,5 * b√2 = |
| b2 |
| | 2 | | 2 | | 2 | |
30 lis 15:21
corn:
H = h +1/2|CB|, skąd wiedziałeś jak to zapisać?

Poza tym dzięki bo resztę rozumiem
30 lis 15:41
Godzio:
| | 1 | |
Wysokość ABC zawiera się w wysokości KLM może źle trochę zapisałem |
| |CB| ale powstał |
| | 2 | |
kwadrat więc odległość środka kwadratu od środka jego boku to połowa boku tego kwadratu
30 lis 15:44
Godzio: Teraz zauważyłem że
| | 1 | | 1 | |
H = ... = |
| b√2 + |
| b √2 = b √2, popraw sobie  |
| | 2 | | 2 | |
30 lis 15:45
 h −− wysokość trójkąta ABC
|KM| = x
|LA| = H
x = b√2 (2 * połowa przekątnej kwadratu o boku b)
h −− wysokość trójkąta ABC
|KM| = x
|LA| = H
x = b√2 (2 * połowa przekątnej kwadratu o boku b)
 Poza tym dzięki bo resztę rozumiem
Poza tym dzięki bo resztę rozumiem
