geometria, dowod. Proszę o pomoc arigatou: Dany jest trojkat ABC w ktorym |AC|=|BC|. Punkt D jest spodkiem wysokosci poprowadzonej z wierzcholka C, punkt E jest srodkiem boku BC a |CD|=|DE|. Udowodnij, ze trojkat CDE jest rownoboczny.

Al Capone:

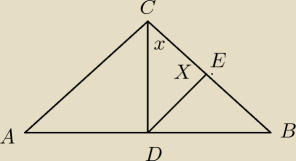
	CE		DE		EB=CE		DE
Tw sinusów		=		⋀		=
	sin(180o − 2x)		sinx		sin(2x−90o)		sin(90o−x)

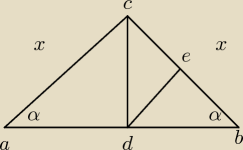
Marcin W: przyjmijmy oznaczenia jak na rys: Odcinek | de | łączy srodki bokow trójkata zatem ma długosc równą polowie boku ac czyli 0,5x. ce jest polową boku cb zatem ma tez 0,5x. z tresci zadania wiemy ze cd=ce zatem cd trez ma dlugosc 0,5x Zatem wszystkie boki trojkata cde maja dlugosc 0,5x zatem jest on rownoboczny.

Kaczucha(al capone): c.d.

sin(2x−90o)		sin(90o−x)
	=
sin(180o−2x)		sinx

Rozwiązanie powyższego równania w dziedzinie : cosx=¹₂ ;x=60^o Czyli trójkąt CDE ma wszystkie kąty równe 60^o;jest równoboczny To x [X] na rysunku to to samo,tylko tak się narysowało

Marcin W: al capone ...