Funkcja logarytmiczna Zielonooka19: bardzo proszę sprawdzenie i poprawę: Zbadać przebieg zmienności i narysować wykres: f(x) = ln²x −lnx Dziedzina: x∊(0, +∞) Granice na końcach przedziałów: lim_x→+∞ ln²x −lnx = +∞ lim_x→0⁺ ln²x −lnx = +∞ lim_x→0⁻ ln²x −lnx = +∞ Asymptoty: pionowe x = 0 (dla x →+∞) poziome − bark ukośne − brak /a=0/ ekstrema lokalne / monotoniczność:

	1		1		2lnx−1
f'(x) = (ln2x −lnx)' = 2lnx *		−		=
	x		x		x

znak funkcji zależy do licznika: 2lnx − 1 = 0 2lnx = 1 √e = x f rosnąca dla x∊(√e, +∞) f malejąca dla x∊(0, √e) x_min = √e y_min = f(x_min) Nie mogę policzyć jeszcze f''(x) / wypukłości i punktu przegięcia, aczkolwiek nawet bez tego nie bardzo wychodzi mi wykres.. Będę wdzięczna za sprawdzenie i ewentualne pokazanie błędów...

Zielonooka19: może jednak ktoś zerknie... ?

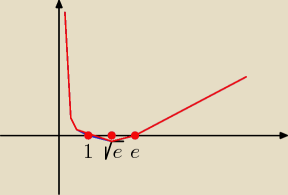
Bogdan: 1. jeśli D_f: x∊R₊, to nie ma potrzeby wyznaczać granicę przy x→0⁻ 2. warto wyznaczyć miejsca zerowe: ln²x − lnx = 0

Zielonooka19: Dziękuję Wyszedł mi podobny wykres tylko jakiś ostry dziubek. 1. no tak 2. wyliczyłam, tylko zapomniałam tu wpisać. Uff

Bogdan: Tu można zamieścić tylko szkic wykresu, oczywiście nie ma żadnych "ostrych dziubków".

Zielonooka19: Wiem, "ostry dziubek" wyszedł odruchowo. A powiedz mi, jeśli mam np:

	1+lnx
f(x) =
	x

to jak z dziedziną? nadal x ∊ R₊ ?

Bogdan: Tak, bo z lnx wynika, że x∊R₊