Wyznacz równania stycznych do okręgu goseska: Wyznacz równania stycznych do okręgu x² − 4x + y² − 2y − 4 = 0 równoległych do osi OY. (Zadanie pochodzi z próbnej matury z Operonem z listopada 2009; wyznaczyłam środek okręgu S=(4,2) i promień r=2, nie wiem, co dalej, proszę mnie oświecić)

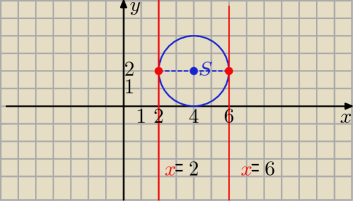
Eta: S( 4,2) r= 2 styczne równoległe do osi OY mają równanie: x= a => x−a=0 odległość d środka S(4,2) od stycznej to: d= r= 2

	| 4*1+2*0 −a|
d=		= 2
	√12 + 02

| 4−a|= 2 => 4−a=2 lub 4−a= −2 a= 2 lub a= 6 zatem są dwie takie styczne spełniające warunki zadania x= 2 lub x= 6 co można sprawdzić na załączonym "obrazku"

Gustlik: x² − 4x + y² − 2y − 4 = 0 x² + y² − 4x − 2y − 4 = 0 x² + y² + Ax + By + C= 0

	A		−4
a=−		=−		=2
	2		2

	B		−2
b=−		=−		=1
	2		2

r=√a²+b²−C=√2²+1²−(−4)=√4+1+4=√9=3 S=(2, 1), r=3 Zatem styczne równoległe do osi OY będą to proste "pionowe" i muszą być oddalone o 3 od środka okregu, czyli: x=2−3=−1 lub x=2+3=5 Odp: x=−1 i x=5.