prosze o pomoc:) Ewelina: Napisz równanie symetralnej odcinka o końcach:A=(2,4),B=(4,6).

M:

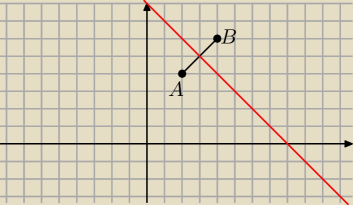
Podstawy Geometrii: A=(2,4) B=(4,6) √x_s−2)²+(4−y_s)²=√(4−x_s)²+(6−y_s)² (x_s−2)²+(4−y_s)²=(4−x_s)²+(6−y_s)² x_s²−4x_s+4+16−8y_s+y_s²=16−8x_s+x_s²+36−12y_s+y_s² −4x_s+8x_s−8y_s+12y_s−32=0 4x_s+4y_s−32=0 4x+4y−32=0 postac ogólna 4y=−4x+32 y=−x+8 postac kierunkowa 4x+4y=32

4x		4y		32
	+		=
32		32		32

x		y
	+		=1
8		8

czy dobrze wyznaczyłem postać odcinkową ?

Mila: Symetralna odcinka − zbiór wszystkich punków jednakowo odległych od końców odcinka. A=(2,4),B=(4,6) (x−2)²+(y−4)²=(x−4)²+(y−6)²⇔ y=−x+8 rysunek j.w.

Jolanta: I przyszła Mila i pozamiatane Podobne zadanie trzecia klasa technikum 1) policzenie współrzędnych środka odcinka AB 2)policzenie współczynnika kierunkowego prostej ,na której leży odcinek AB,żeby policzyć współczynnik kierunkowy symetralnej 3)podstawienie do wzoru kierunkowego prostej współrzędnych środka i współczynnika kierunkowego