oblicz Anja :): oblicz A ∪ B, A \ B, B \ A oraz A ∩ B jeżeli: a) A={−2,0,1,3,5} B={−1,0,3,5,7} b) A=(−3;5) B=<0,7)

sushi_ gg6397228: popatrz na lekture i poprobuj sama https://matematykaszkolna.pl/strona/1059.html https://matematykaszkolna.pl/strona/8.html

Anja :): to nie takie proste jak sie jest tyle lat po szkole pozdrawiam i dziekuje za pomoc

sushi_ gg6397228: AuB= to wypisujemy wszystkie elementy co sa w obu zbiorach AnB = to wypisujemy elementy co sie powtarzaja w obu zbiorach

Anja :): to teraz mam pytanie czy to dobrze zrobilam a) AuB = { −2, −1, 0, 1, 3, 5, 7 } AnB = { 0, 3, 5 } A\B = { −2, 1 } B\A = { −1, 7 } oraz czy musza byc do tego wykresy

Anja :): z tym punktem b) mam problem nie wiem jak bo patrzac na to co podpowiadasz to nie ma tam takich przykładów z takimi nawiasami

sushi_ gg6397228: AuB i AnB dobrze A\B mozna rozpisac A− (AnB) lub po prostu to co jest w "A" a nie ma w "B"

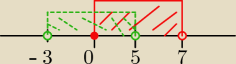
sushi_ gg6397228: pomysl ze te dwa kolory to dwie rozne trasy autobusowe (A− kolor zielony, B− kolor czerwony) AuB= chcemy jak najdalej pojechac autobusem AnB== gdzie obie linie sie pokrywaja domkniety ∩ domkniety daje " domkniety" ( w pozostalych przypadkach otwarty) A\B gdzie tylko jedziemy linia A domkniety\ otwarty daje domkniety ( pozostale przypadki otwarty) B\A gdzie tylko linia B

Anja :): a podpunkt b)AuB= −3,7 AnB=0,5 A\B=−3,5 B\A=0,7 tylko teraz czy to jest dobrze i jakie maja byc nawiasy? bo w podpunkcje sa rozne nawiasy?

think: na wykresie kółkiem niezamalowanym oznacza się punkt otwarty a kółkiem zamalowanym punkt domknięty.

Anja :): dziekuje