enter: Wyznacz te wartości parmateru m dla których a) zbiór rozwiązań nierówności mx²-x+1-m<0 zawiera się w zbiorze rozwiązań nierówności 0≤x≤1 odp: x∈<0,5;1> gdzie robię błąd? rozpatruję przypadki: 1. {a>0 ⇔ m>0 {Δ>0 ⇔ m∈R-{1/2} {f(0)≤0 ⇔ m∈<1,∞) {f(1)≤0 ⇔m∈R {x_w∈<0,1> ⇔ (-∞,0)U(1/2;∞) biorę część wspólną i otrzymuję: m∈(1,∞) 2. {a<0⇔m<0 {Δ<0⇔m∈O (zb pusty) 3. {a=0⇔m=0 {b=0⇔-1=0|sprzeczne {c<0 (zb pusty) 4. {a=0⇔m=0 {b>0⇔-1>0|sprzeczne {f(0)<0 {f(1)≤0 (zb pusty) 5. {a=0⇔m=0 {b<0⇔-1<0 {f(0)≤0⇔m∈<1,∞) {f(1)<0⇔ m∈ O (zb pusty) z całości wynika że błąd jest w pierwszym przypadku... prosze o pomoc

Basia: a po co to wszystko Enterku ? po prostu to rozwiązujemy mx²-x+1-m<0 1. m=0 -x +1<0 -x < -1 x>1 x∈(1; +∞) a część wspólna z <0;1> to zbiór pusty czyli m=0 odpada 2. m#0 Δ = (-1)² -4m(1-m) Δ = 1 - 4m +4m² = 4m² -4m +1 = (2m -1)² (2m-1)² ≥ 0 czyli dla m#0 równanie zawsze ma rozwiązanie √Δ = |2m-1| 2.1 2m-1≥0 ⇔ 2m≥ 1 ⇔ m ≥ 1/2 ------------------------------------------------------ wtedy √Δ =2m-1 x₁ = (1 - 2m +1) / 2m = 2(1-m)/2m = (1-m)/m x₂ = (1+2m-1)/2m = 1 x₂ spełnia warunki zadania niezależnie od m 0 ≤ x₁ ≤1 (1-m)/m ≥ 0 i (1-m)/m≤1 rozw.1 jest przedział <0; 1>n<1/2; +∞) = <1/2 ; 1> rozw.2 (1-m)/m -1≤ 0 (1-m -m)/m ≤0 (1-2m)/m ≤0 rozw.2 jest <0; 1/2>n<1/2; +∞) = {1/2} spełnione muszą być obie czyli cz.wsp. (1) i (2) czyli tylko m=1/2 ================================================================ 2.2 2m-1<0 ⇔ 2m< 1 ⇔ m < 1/2 ------------------------------------------------------ wtedy √Δ =-2m+1 x₁ = (1 + 2m -1) / 2m = 2m/2m = 1 x₂ = (1-2m+1)/2m = 2(1-m)/2m = (1-m) / m x₁ spełnia warunki zadania niezależnie od m 0 ≤ x₂ ≤1 (1-m)/m ≥ 0 i (1-m)/m≤1 rozw.1 jest przedział <0; 1>n(-∞ ; 1/2) = <0; 1/2) rozw.2 (1-m)/m -1≤ 0 (1-m -m)/m ≤0 (1-2m)/m ≤0 rozw.2 jest <0; 1/2>n(-∞; 1/2) = <0 ; 1/2) spełnione muszą być obie czyli cz.wsp. (1) i (2) czyli tylko m ∈ <0 ; 1/2) ================================================================ z 2.1 mamy m=1/2 z 2.2 mamy m∈<0 ; 1/2) co w sumie daje m∈ <0 ; 1/2> ======================= sprawdź Enterku rachunki

Basia: wyszło mi jak widzisz inmaczej, ale o to tu chodzi przeliczę jeszcze raz na papierze, ale to za chwilę

enter: hmm Basiu, dziękuję Ci bardzo, przemyślałam to (dlatego tak długo milczałam i zrozumiałam. Jednak nie czuję się zbyt pewnie, ponieważ moje własne rozumowanie jest mi bliższe... czy mogłabyś jednak jeszcze raz rzucić okiem tylko na ten pierwszy przypadek i zobaczyć gdzie robię błąd? No chyba, ze nie robię... bo to by oznaczało, że całe rozumowanie jest złe

Basia: no już wiem gdzie zrobiłam błąd 1. jest dobrze 2. m#0 Δ = (-1)2 -4m(1-m) Δ = 1 - 4m +4m2 = 4m2 -4m +1 = (2m -1)2 (2m-1)2 ≥ 0 czyli dla m#0 równanie zawsze ma rozwiązanie √Δ = |2m-1| 2.1 2m-1≥0 ⇔ 2m≥ 1 ⇔ m ≥ 1/2 ------------------------------------------------------ wtedy √Δ =2m-1 x1 = (1 - 2m +1) / 2m = 2(1-m)/2m = (1-m)/m x2 = (1+2m-1)/2m = 1 x2 spełnia warunki zadania niezależnie od m 0 ≤ x1 ≤1 (1-m)/m ≥ 0 i (1-m)/m≤1 rozw.1 jest przedział <0; 1>n<1/2; +∞) = <1/2 ; 1> rozw.2 (1-m)/m -1≤ 0 (1-m -m)/m ≤0 (1-2m)/m ≤0 tu było źle rozw.2 jest [ (-∞; 0>U<1/2 ; +∞) ]n<1/2; +∞) = <1/2 ; +∞) spełnione muszą być obie czyli cz.wsp. (1) i (2) czyli tylko m∈<1/2 ; 1> ================================================================ 2.2 2m-1<0 ⇔ 2m< 1 ⇔ m < 1/2 ------------------------------------------------------ wtedy √Δ =-2m+1 x1 = (1 + 2m -1) / 2m = 2m/2m = 1 x2 = (1-2m+1)/2m = 2(1-m)/2m = (1-m) / m x1 spełnia warunki zadania niezależnie od m 0 ≤ x2 ≤1 (1-m)/m ≥ 0 i (1-m)/m≤1 rozw.1 jest przedział <0; 1>n(-∞ ; 1/2) = <0; 1/2) rozw.2 (1-m)/m -1≤ 0 (1-m -m)/m ≤0 (1-2m)/m ≤0 rozw.2 jest [ (-∞;0> U <1/2; +∞) ]n(-∞; 1/2) = (-∞; 0> spełnione muszą być obie czyli cz.wsp. (1) i (2) czyli tylko m =0 ale to sprzeczne z założeniem bo rozważamy przypadek m#0 =============================================================== z 2.1 mamy m∈<1/2 ; 1> z 2.2 zbiór pusty co w sumie daje m∈ <1/2 ; 1> =======================

ola: 2. {a<0⇔m<0 {Δ<0⇔m∈O (zb pusty) dlaczego?

ola: zdecydowanie rozwiązanie Basi jest logiczniejsze

enter: olu moje rozwiązanie sprowadziło się do tego, ze namalowałam sobie os i wszystkie możliwości. 2. to przypadek kiedy parabola ma łapki w dół (a<0) i kiedy nie ma miejsc zerowych, bo to warunek, aby w tym przedziale wszystkie rozwiązania były mniejsze od zera Miomo, że uważasz że rozw Basi jest logiczne (absolutnie tego nie podwarzam) chciałabym aby ktoś sprawdził moje

Basia: jeżeli a>0 i Δ≥0 i pierwaistki maja się znaleźć w przedziale <0 ; 1> to musi odwrotnie f(0)≥0 i f(1)≥1 -------------------------- narysuj to; ramiona do góry; pierwaiastki (lub jeden pierwiastek) w <0; 1> no i to jest Twój błąd ------------------------------ a<0 i Δ≥0 to f(0)≤ i f(1)≤ 0 też narysuj; ramiona w dół przypadek m=0 wystarczy rozpatrzyć raz patrz moje rozwiązanie ale pomysł Enterku znakomity tylko przydałoby się go lepiej opisać, bo na pierwszy rzut oka nie każdy zrozumie o co Ci chodziło

enter105: super Basiu, dziękuję bardzo

wdzmach: 4m²+1=4m

Krzysiek : 4m²−4m+1=0 i jedziesz

Mila: Dołączam do Was. Zbiór rozwiązań nierówności mx²−x+1−m<0 zawiera się w zbiorze rozwiązań nierówności 0≤x≤1 f(x)=mx²−x+1−m 1) m=0 f(x)=−x+1 −x+1<0⇔−x<−1⇔x>1 funkcja przyjmuje wartości ujemne dla x∊(1;∞) zatem m=0 nie spełnia warunków zadania. 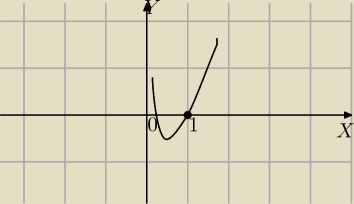2) dla m≠0 mamy trójmian kwadratowy f(0)=1−m i f(1)=0 zatem x=1 jest miejscem zerowym trójmianu dla każdego m≠0 Δ=(2m−1)²≥0 dla każdego m∊R Rozważamy tylko przypadek Δ>0 Sytuacja która spełni warunki zadania na ilustracji:⇔ m>0 i drugi pierwiastek znajduje się w przedziale<0;1>

	1		1		1
⇔		≤xw<1⇔		≤		<1
	2		2		2m

	1
stąd m>		i m≤1
	2

	1
dla m=		mamy sytuację
	2

	1		1		1		1
f(x)=		x2−x+1−		⇔f(x)=		x2−x+
	2		2		2		2

1		1
	x2−x+		<0⇔x∊Φ
2		2

odp.

	1
m∊(		;1>
	2