coś trudniejszego Agata: Ze środka ściany sześcianu o krawędzi a poprowadzono prostą prostopadłą do przekatnej szescianu, Wyznacz dlugosc odcinkow, na jakie ta prosta podzielila przekatna szescianu.

Anna: Już Ci piszę, Agato.

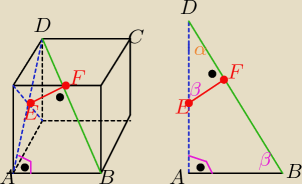
kometa: ΔABD ~ Δ EFD z cechy ( k,k,k) ( bo są prostokątne i mają wspólny kąt α IABI=a IADI = a√2 −−− dł. przekątnej kwadratu IDEI= ¹₂IADI=^a₂ √2 −−− z treści zad oraz I BDI = a√3 −−−− dł. przekątnej głównej sześcianu to

	IDFI		IADI
		=
	IDEI		IDBI

wyznacz: IDFI =...... i IBFI = IDBI − IDFI=........ dokończ obliczenia

Anna: Dane: a. Szuk. : IEKI, IKCI Z ΔACE: d² = a² +d₁² d² = a² + (a√2)² ⇒ d² = 3a² ⇒ d = a√3 ΔACE ∼ ΔKOC (cecha kk)

	a√2		IKCI
Stąd:		=
	d		a√2   2

a√2		IKCI		a√2   a√2*   2		a
	=		⇒ IKCI =		=		=
a√3		a√2   2		a√3		√3

	a√3
	3

	a√3		2a√3
IEKI = d − IKCI = a√3 −		=
	3		3