Oblicz objetosc graniastosłupa Agata: Oblicz objetosc graniastosłupa prawidłowego trojkatnego, w którym długość krawędzi podstawy jest rowna 20 cm oraz kat nachylenia przekątnej ściany bocznej do sasiedniejsciany bocznej ma miarę 60st. Pomocy!

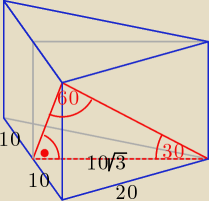
Bogdan: Czy ten rysunek pomoże?

Agata: A mógłbyś coć więcej?

dero2005: Oblicz przekątną ściany bocznej ^10√3_d = cos 30 = ^√3₂ oblicz wysokośc h z Pitagorasa Oblicz pole podstawy oblicz objętość

Agata: nie wiem jak mam policzyć przekatna ściany bocznej

dero2005: Dane krawędź a = 20 obliczam przekątną ściany bocznej ad = sin 60 = √32 d = 40√33 obliczam h h = √d2 − a2 = 20√33 obliczam wysokość podstawy h1 h1 = a√32 = 10√3 obliczam pole podstawy Pp = a*h12 = 100√3 obliczam objętość V = Pp*h = 2000 cm3

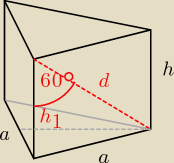
Bogdan: dero2005 − na Twoim rysunku kąt o mierze 60^o nie jest kątem między przekątną ściany bocznej i sąsiednią ścianą boczną, to jest kąt między przekątną ściany bocznej i krawędzią boczną.

dero2005: Bogdan z Twojego rys przekątna ściany bocznej jest równa długości podstawy czyli h = 0

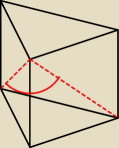
dero2005: może ten rys powinien tak wyglądać?

Bogdan: Czy widzisz dero2005 coś nieprawidłowego w moim rysunku? Jeśli tak, to wskaż to miejsce.

Bogdan: Na kolejnym Twoim rysunku dero2005 zaznaczyłeś kąt między przekątnymi ścian bocznych, ale nie kąt między przekątną ściany bocznej i sąsiednią ścianą boczną.

Agata: obliczenia sa w porzadku?

dero2005: do Bogdan Z czerwonego trójkąta na rys wynika że, ^10√3_d = cos 30 = ^√3₂ d*√3 = 20√3 d = 20 → przekątna ściany bocznej, której bok (krawędź podstawy) = 20 to ile wyjdzie wysokość?

Bogdan:

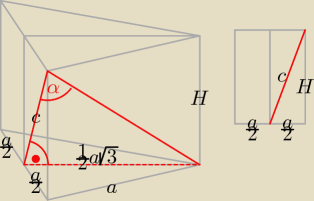
c		1		3
	= ctgα ⇒ c =		a√3ctgα ⇒ c2 =		a2ctg2α
1   a√3 2		2		4

Z wzoru Pitagorasa:

	a		3		a2		a2(3ctg2α − 1)
H2 = c2 − (		)2 =		a2ctg2α −		=
	2		4		4		4

	1
H =		a√ 3ctg2α − 1
	2

	√3		3		1
Dla α = 60o: ctg60o =		⇒ ctg2α =		=
	3		9		3

	1
H =		a√ 3 * (1/3) − 1 = 0
	2

Biorąc dane z zadania trzeba stwierdzić, że objętość graniastosłupa V = 0.

Bogdan: Jakie dane w zadaniu − takie rozwiązanie

Agata: yhym, czyli twoje Bogdan roziwązanie jest ok tak?

niematurzysta: Cz ktoś może wie, dlaczego kąt między przekątną ściany boczne a sąsiednia ścianą boczną to akurat ten na rys Bogdana. Wiem, że to dobry kąt, ale czemu bierzemy odcinke łączący wierzchołek ściany bocznej ze środkiem sąsiedniej ścniany?

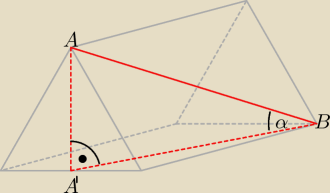
Bogdan: Jeśli położymy graniastosłup na ścianie bocznej, to łatwiej jest zauważyć ten kąt. Punkt A' jest rzutem prostokątnym końca A przekątnej AB na ścianę z odcinkiem A'B.

Mel: wydaję mi się, że w tym zadaniu podany kąt między przekątną ściany bocznej a sąsiednią ścianą wynosi 45^o . przynajmniej ja mam tak zapisane. czy wtedy V= 1000 √6 ?